Question Number 51151 by peter frank last updated on 24/Dec/18

$${Find}\:{the}\:{equation}\:{of} \\ $$$${tangent}\:{to}\:{the}\:\:{ellipse} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} =\mathrm{4}\:{which}\:{are} \\ $$$${perpendicular}\:{to}\:{the}\: \\ $$$${line}\:\mathrm{2}{x}−\mathrm{3}{y}=\mathrm{1} \\ $$$$ \\ $$$$\ast{merry}\:{X}−{mas}\:{and}\:{happy}\:{new}\:{year}\ast \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
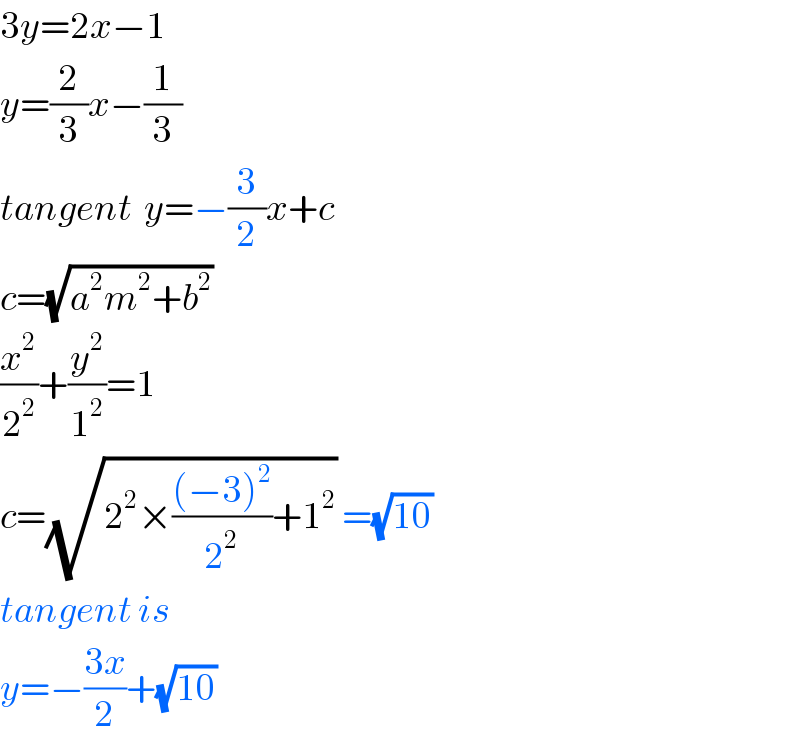
$$\mathrm{3}{y}=\mathrm{2}{x}−\mathrm{1} \\ $$$${y}=\frac{\mathrm{2}}{\mathrm{3}}{x}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${tangent}\:\:{y}=−\frac{\mathrm{3}}{\mathrm{2}}{x}+{c} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} }\: \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} }=\mathrm{1} \\ $$$${c}=\sqrt{\mathrm{2}^{\mathrm{2}} ×\frac{\left(−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\mathrm{1}^{\mathrm{2}} }\:=\sqrt{\mathrm{10}}\: \\ $$$${tangent}\:{is} \\ $$$${y}=−\frac{\mathrm{3}{x}}{\mathrm{2}}+\sqrt{\mathrm{10}}\: \\ $$
