Question Number 120452 by john santu last updated on 31/Oct/20
$${Find}\:{the}\:{equation}\:{of}\:{the}\:{line}\:{tangent}\:{to}\:{the}\:{parametric} \\ $$$${curve}\:{given}\:{by}\:{the}\:{equations}\:\begin{cases}{{x}=\left(\mathrm{1}+{t}^{\mathrm{3}} \right)^{\mathrm{4}} +{t}^{\mathrm{2}} }\\{{y}={t}^{\mathrm{5}} +{t}^{\mathrm{2}} +\mathrm{2}}\end{cases}\:{at}\:{t}=\mathrm{1} \\ $$
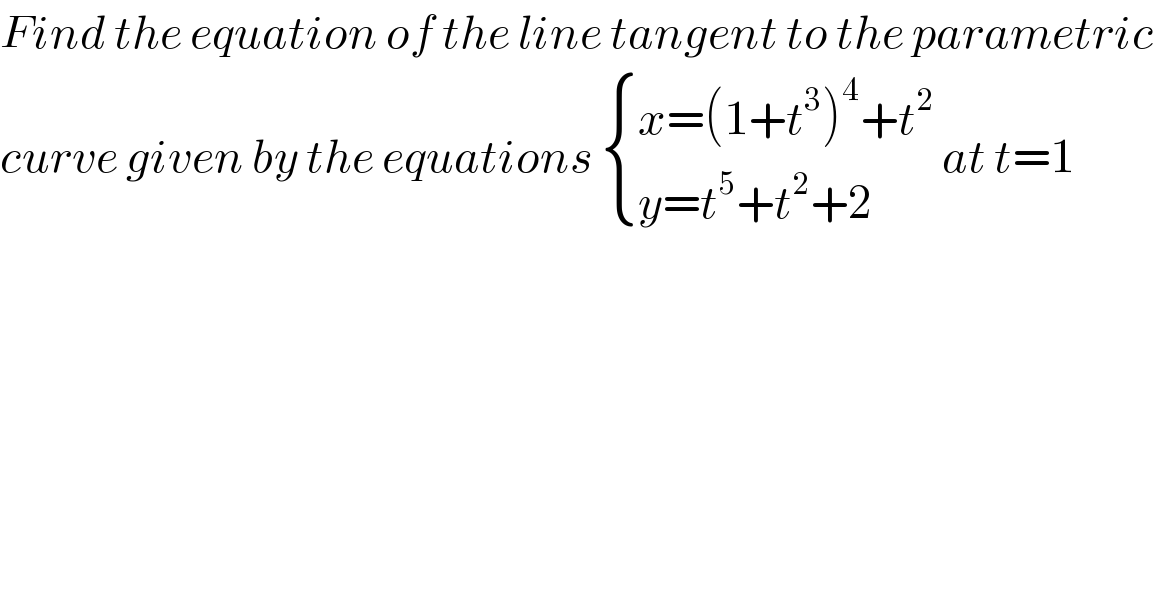
Answered by physicstutes last updated on 31/Oct/20
![x = (1 + t^3 )^4 + t^2 , when t = 1, x = 17 ⇒ (dx/dt) = 12t^2 (1+t^3 )^3 + 2t also y = t^5 + t^2 + 2 when t = 1, y = 4 ⇒ (dy/dt) = 5t^4 + 2t (dy/dx) = (dy/dt)×(dt/dx) = ((5t^4 +2t)/(12t^2 (1+t^3 )^3 +2t)) ((dy/dx))_(t=1) = (5/(98)) y − 4 = (5/(99))(x−17) 98(y−4) = 5(x−17) [mistakes corrected]](https://www.tinkutara.com/question/Q120453.png)
$$\:{x}\:=\:\left(\mathrm{1}\:+\:{t}^{\mathrm{3}} \right)^{\mathrm{4}} \:+\:{t}^{\mathrm{2}} \:,\:\mathrm{when}\:{t}\:=\:\mathrm{1},\:{x}\:=\:\mathrm{17} \\ $$$$\Rightarrow\:\frac{{dx}}{{dt}}\:=\:\mathrm{12}{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{3}} \right)^{\mathrm{3}} +\:\mathrm{2}{t}\: \\ $$$$\mathrm{also}\:{y}\:=\:{t}^{\mathrm{5}} \:+\:{t}^{\mathrm{2}} \:+\:\mathrm{2}\:\mathrm{when}\:{t}\:=\:\mathrm{1},\:{y}\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\frac{{dy}}{{dt}}\:=\:\mathrm{5}{t}^{\mathrm{4}} \:+\:\mathrm{2}{t}\:\: \\ $$$$\:\:\:\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}}\:=\:\frac{\mathrm{5}{t}^{\mathrm{4}} +\mathrm{2}{t}}{\mathrm{12}{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{2}{t}} \\ $$$$\left(\frac{{dy}}{{dx}}\right)_{{t}=\mathrm{1}} \:=\:\frac{\mathrm{5}}{\mathrm{98}} \\ $$$$\:\:{y}\:−\:\mathrm{4}\:=\:\frac{\mathrm{5}}{\mathrm{99}}\left({x}−\mathrm{17}\right) \\ $$$$\mathrm{98}\left({y}−\mathrm{4}\right)\:=\:\mathrm{5}\left({x}−\mathrm{17}\right)\:\left[\mathrm{mistakes}\:\mathrm{corrected}\right] \\ $$
Commented by bramlexs22 last updated on 31/Oct/20
$${typo}\:{it}\:{should}\:{be}\:\frac{\mathrm{7}}{\mathrm{98}} \\ $$
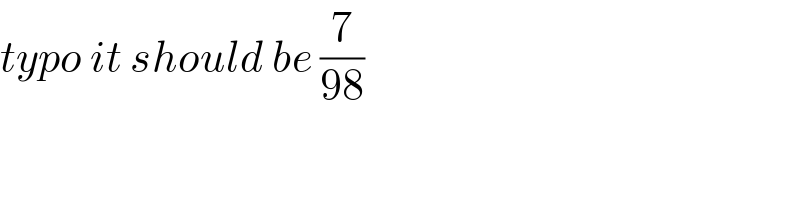
Commented by peter frank last updated on 31/Oct/20
$$\mathrm{help}\:\mathrm{please}\:\mathrm{90208},\mathrm{90030} \\ $$
Answered by bramlexs22 last updated on 31/Oct/20
$${gradient}\:\left({m}\right)=\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}} \\ $$$$\:=\:\frac{\mathrm{5}{t}^{\mathrm{4}} +\mathrm{2}{t}}{\mathrm{12}{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{2}}\:=\:\frac{\mathrm{7}}{\mathrm{98}} \\ $$$${for}\:{t}\:=\:\mathrm{1}\:\rightarrow\begin{cases}{{x}=\mathrm{17}}\\{{y}=\mathrm{4}}\end{cases} \\ $$$${eq}\:{of}\:{line}\:{tangent}\:\mathrm{7}{x}−\mathrm{98}{y}=\mathrm{7}\left(\mathrm{17}\right)−\mathrm{98}\left(\mathrm{4}\right) \\ $$$$\mathrm{7}{x}−\mathrm{98}{y}=\mathrm{119}−\mathrm{392} \\ $$$$\Leftrightarrow\mathrm{7}{x}−\mathrm{98}{y}+\mathrm{273}=\mathrm{0} \\ $$$$ \\ $$