Question Number 183241 by depressiveshrek last updated on 23/Dec/22
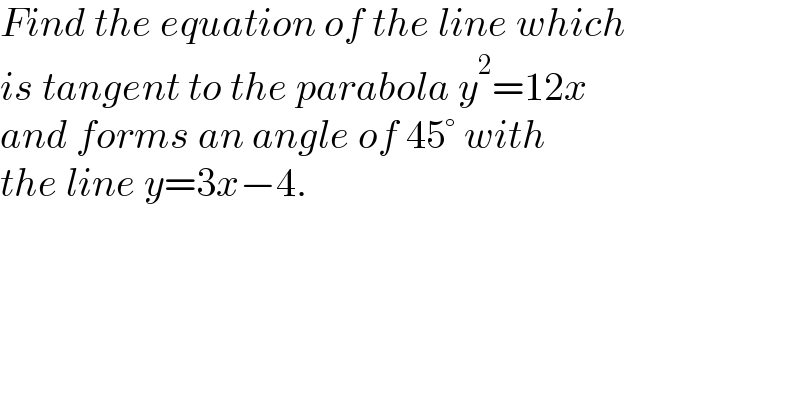
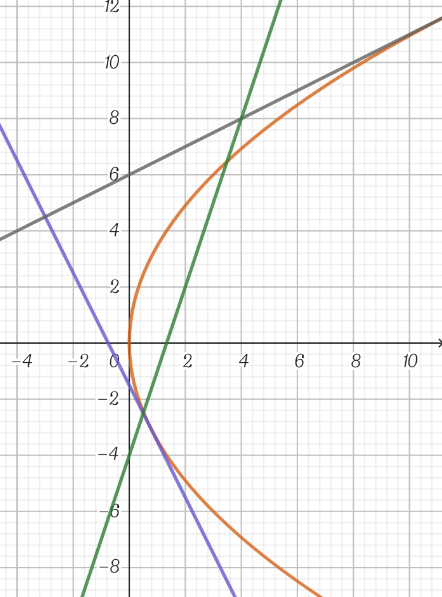
$${Find}\:{the}\:{equation}\:{of}\:{the}\:{line}\:{which} \\ $$$${is}\:{tangent}\:{to}\:{the}\:{parabola}\:{y}^{\mathrm{2}} =\mathrm{12}{x} \\ $$$${and}\:{forms}\:{an}\:{angle}\:{of}\:\mathrm{45}°\:{with}\: \\ $$$${the}\:{line}\:{y}=\mathrm{3}{x}−\mathrm{4}. \\ $$
Answered by cortano1 last updated on 24/Dec/22
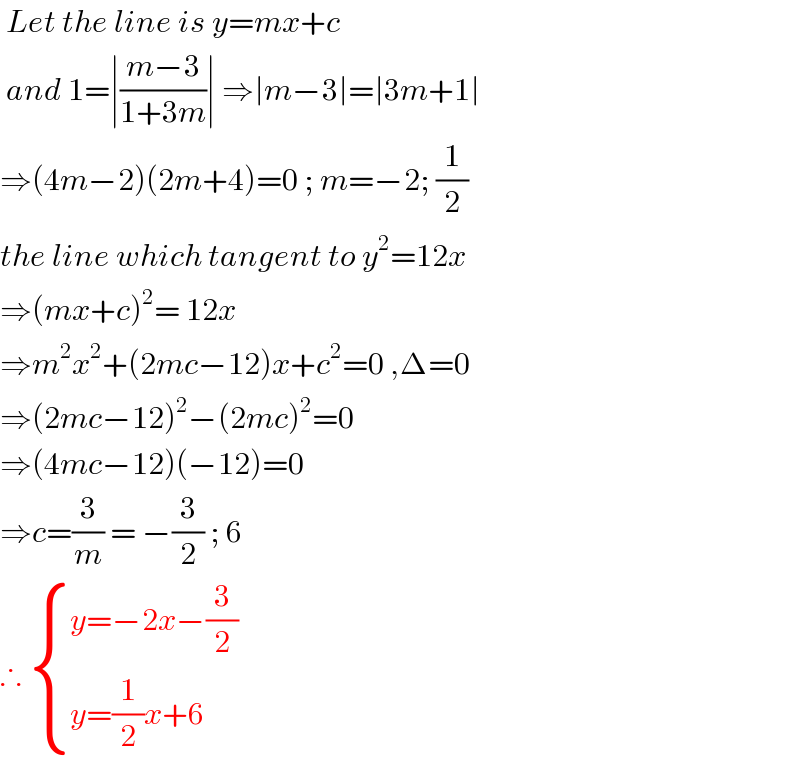
$$\:{Let}\:{the}\:{line}\:{is}\:{y}={mx}+{c} \\ $$$$\:{and}\:\mathrm{1}=\mid\frac{{m}−\mathrm{3}}{\mathrm{1}+\mathrm{3}{m}}\mid\:\Rightarrow\mid{m}−\mathrm{3}\mid=\mid\mathrm{3}{m}+\mathrm{1}\mid \\ $$$$\Rightarrow\left(\mathrm{4}{m}−\mathrm{2}\right)\left(\mathrm{2}{m}+\mathrm{4}\right)=\mathrm{0}\:;\:{m}=−\mathrm{2};\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${the}\:{line}\:{which}\:{tangent}\:{to}\:{y}^{\mathrm{2}} =\mathrm{12}{x} \\ $$$$\Rightarrow\left({mx}+{c}\right)^{\mathrm{2}} =\:\mathrm{12}{x} \\ $$$$\Rightarrow{m}^{\mathrm{2}} {x}^{\mathrm{2}} +\left(\mathrm{2}{mc}−\mathrm{12}\right){x}+{c}^{\mathrm{2}} =\mathrm{0}\:,\Delta=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{mc}−\mathrm{12}\right)^{\mathrm{2}} −\left(\mathrm{2}{mc}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{4}{mc}−\mathrm{12}\right)\left(−\mathrm{12}\right)=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{3}}{{m}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\:;\:\mathrm{6} \\ $$$$\therefore\:\begin{cases}{{y}=−\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{2}}}\\{{y}=\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{6}\:}\end{cases} \\ $$
Commented by cortano1 last updated on 24/Dec/22