Question Number 95206 by hardylanes last updated on 23/May/20

$${find}\:{the}\:{equation}\:{of}\:{the}\:{straight}\:{line}\:{which} \\ $$$${passes}\:{through}\:{the}\:{point}\:{of}\:{intersertion}\:{of} \\ $$$${the}\:{lines}\:\mathrm{4}{x}+\mathrm{3}{y}+\mathrm{19}=\mathrm{0}\:{and}\:\mathrm{12}{x}−\mathrm{5}{y}+\mathrm{3}=\mathrm{0} \\ $$$${and}\:{has}\:{a}\:{y\_intercept}\:{of}\:\mathrm{2} \\ $$
Commented by PRITHWISH SEN 2 last updated on 24/May/20
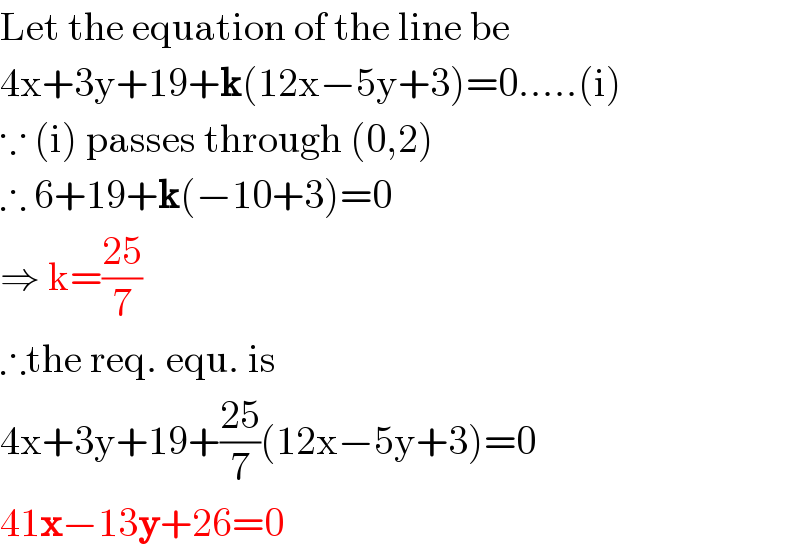
$$\mathrm{Let}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{be} \\ $$$$\mathrm{4x}+\mathrm{3y}+\mathrm{19}+\boldsymbol{\mathrm{k}}\left(\mathrm{12x}−\mathrm{5y}+\mathrm{3}\right)=\mathrm{0}…..\left(\mathrm{i}\right) \\ $$$$\because\:\left(\mathrm{i}\right)\:\mathrm{passes}\:\mathrm{through}\:\left(\mathrm{0},\mathrm{2}\right)\: \\ $$$$\therefore\:\mathrm{6}+\mathrm{19}+\boldsymbol{\mathrm{k}}\left(−\mathrm{10}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{k}=\frac{\mathrm{25}}{\mathrm{7}} \\ $$$$\therefore\mathrm{the}\:\mathrm{req}.\:\mathrm{equ}.\:\mathrm{is} \\ $$$$\mathrm{4x}+\mathrm{3y}+\mathrm{19}+\frac{\mathrm{25}}{\mathrm{7}}\left(\mathrm{12x}−\mathrm{5y}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{41}\boldsymbol{\mathrm{x}}−\mathrm{13}\boldsymbol{\mathrm{y}}+\mathrm{26}=\mathrm{0} \\ $$
Answered by bobhans last updated on 24/May/20

$$\mathrm{the}\:\mathrm{point}\:\mathrm{intersection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lines}\:\mathrm{is}\:\left(−\frac{\mathrm{13}}{\mathrm{7}},−\:\frac{\mathrm{27}}{\mathrm{7}}\right) \\ $$$$\mathrm{and}\:\mathrm{y}−\mathrm{intercept}\:\mathrm{2}\:\Rightarrow\:\mathrm{The}\:\mathrm{equation}\:\mathrm{of}\: \\ $$$$\mathrm{straight}\:\mathrm{line}\:\mathrm{with}\:\mathrm{slope}\:=\:\frac{\mathrm{2}+\frac{\mathrm{27}}{\mathrm{7}}}{\mathrm{0}+\frac{\mathrm{13}}{\mathrm{7}}}=\:\frac{\mathrm{41}}{\mathrm{13}} \\ $$$$.\:\mathrm{so}\:\mathrm{the}\:\mathrm{eq}\:\mathrm{of}\:\mathrm{line} \\ $$$$\mathrm{is}\:\Rightarrow\mathrm{41x}\:−\mathrm{13y}\:=\:−\mathrm{26} \\ $$
