Menu Close

Find-the-equation-of-the-two-lines-throught-2-3-which-makes-45-with-the-line-2x-y-2-hence-find-the-cosine-of-the-acute-between-the-lines-l-1-y-2x-5-0-and-l-2-y-x-6-leave-your-ans

Tinku Tara 0 Comments
Pin




Question Number 38049 by Rio Mike last updated on 21/Jun/18
Find the equation of the two lines throught (2,−3) which makes 45° with the line 2x − y = 2..hence find the cosine of the acute between the lines l_1 : y− 2x + 5=0 and l_2 : y − x + 6 (leave your answer in surd form)
$${Find}\:{the}\:{equation}\:{of}\:{the}\:{two}\:{lines} \\ $$$${throught}\:\left(\mathrm{2},−\mathrm{3}\right)\:{which}\:{makes}\:\mathrm{45}° \\ $$$${with}\:{the}\:{line}\:\mathrm{2}{x}\:−\:{y}\:=\:\mathrm{2}..{hence} \\ $$$${find}\:{the}\:{cosine}\:{of}\:{the}\:{acute}\:{between} \\ $$$${the}\:{lines}\:{l}_{\mathrm{1}} :\:{y}−\:\mathrm{2}{x}\:+\:\mathrm{5}=\mathrm{0}\:{and}\: \\ $$$${l}_{\mathrm{2}} :\:{y}\:−\:{x}\:+\:\mathrm{6}\:\left({leave}\:{your}\:{answer}\:{in}\right. \\ $$$$\left.{surd}\:{form}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18
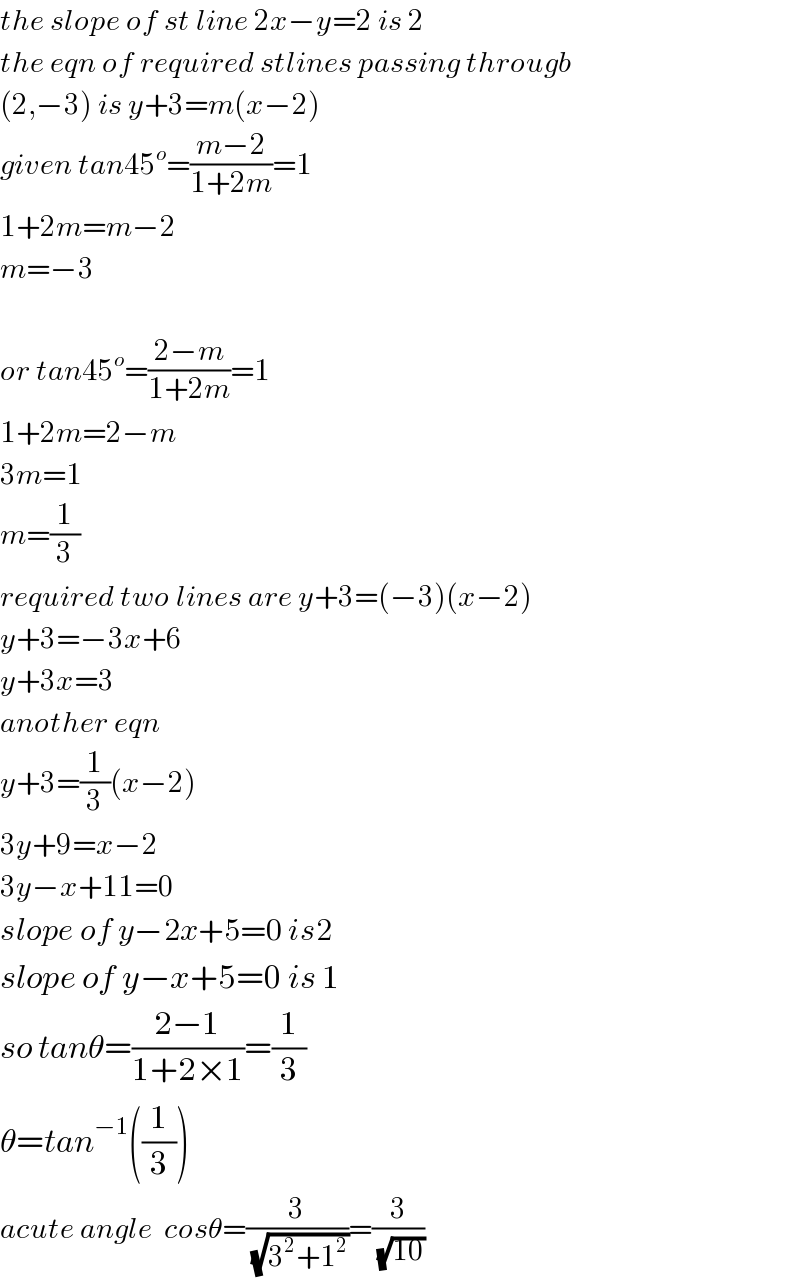
the slope of st line 2x−y=2 is 2 the eqn of required stlines passing througb (2,−3) is y+3=m(x−2) given tan45^o =((m−2)/(1+2m))=1 1+2m=m−2 m=−3 or tan45^o =((2−m)/(1+2m))=1 1+2m=2−m 3m=1 m=(1/3) required two lines are y+3=(−3)(x−2) y+3=−3x+6 y+3x=3 another eqn y+3=(1/3)(x−2) 3y+9=x−2 3y−x+11=0 slope of y−2x+5=0 is2 slope of y−x+5=0 is 1 so tanθ=((2−1)/(1+2×1))=(1/3) θ=tan^(−1) ((1/3)) acute angle cosθ=(3/( (√(3^2 +1^2 ))))=(3/( (√(10))))
$${the}\:{slope}\:{of}\:{st}\:{line}\:\mathrm{2}{x}−{y}=\mathrm{2}\:{is}\:\mathrm{2} \\ $$$${the}\:{eqn}\:{of}\:{required}\:{stlines}\:{passing}\:{througb} \\ $$$$\left(\mathrm{2},−\mathrm{3}\right)\:{is}\:{y}+\mathrm{3}={m}\left({x}−\mathrm{2}\right) \\ $$$${given}\:{tan}\mathrm{45}^{{o}} =\frac{{m}−\mathrm{2}}{\mathrm{1}+\mathrm{2}{m}}=\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}{m}={m}−\mathrm{2} \\ $$$${m}=−\mathrm{3} \\ $$$$ \\ $$$${or}\:{tan}\mathrm{45}^{{o}} =\frac{\mathrm{2}−{m}}{\mathrm{1}+\mathrm{2}{m}}=\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}{m}=\mathrm{2}−{m} \\ $$$$\mathrm{3}{m}=\mathrm{1} \\ $$$${m}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${required}\:{two}\:{lines}\:{are}\:{y}+\mathrm{3}=\left(−\mathrm{3}\right)\left({x}−\mathrm{2}\right) \\ $$$${y}+\mathrm{3}=−\mathrm{3}{x}+\mathrm{6} \\ $$$${y}+\mathrm{3}{x}=\mathrm{3} \\ $$$${another}\:{eqn} \\ $$$${y}+\mathrm{3}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{2}\right) \\ $$$$\mathrm{3}{y}+\mathrm{9}={x}−\mathrm{2} \\ $$$$\mathrm{3}{y}−{x}+\mathrm{11}=\mathrm{0} \\ $$$${slope}\:{of}\:{y}−\mathrm{2}{x}+\mathrm{5}=\mathrm{0}\:{is}\mathrm{2} \\ $$$${slope}\:{of}\:{y}−{x}+\mathrm{5}=\mathrm{0}\:{is}\:\mathrm{1} \\ $$$${so}\:{tan}\theta=\frac{\mathrm{2}−\mathrm{1}}{\mathrm{1}+\mathrm{2}×\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\theta={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${acute}\:{angle}\:\:{cos}\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *