Question Number 22554 by *D¬ B£$T* last updated on 20/Oct/17
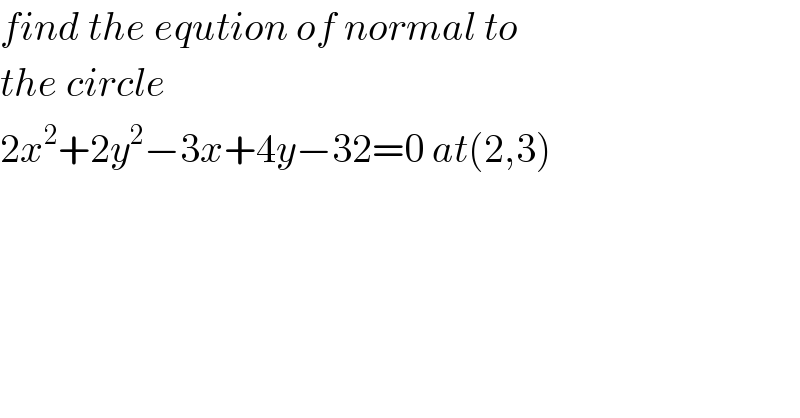
$${find}\:{the}\:{eqution}\:{of}\:{normal}\:{to} \\ $$$${the}\:{circle} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{32}=\mathrm{0}\:{at}\left(\mathrm{2},\mathrm{3}\right) \\ $$
Answered by ajfour last updated on 20/Oct/17
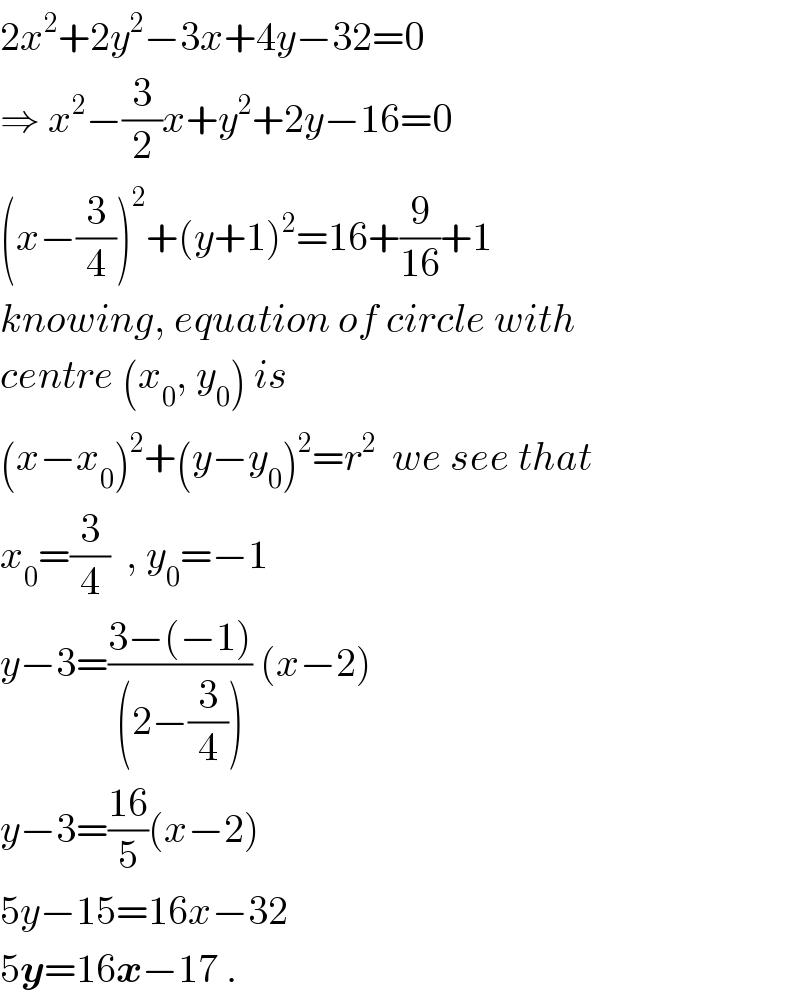
$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4}{y}−\mathrm{32}=\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}{x}+{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{16}=\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{16}+\frac{\mathrm{9}}{\mathrm{16}}+\mathrm{1} \\ $$$${knowing},\:{equation}\:{of}\:{circle}\:{with} \\ $$$${centre}\:\left({x}_{\mathrm{0}} ,\:{y}_{\mathrm{0}} \right)\:{is}\: \\ $$$$\left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +\left({y}−{y}_{\mathrm{0}} \right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:{we}\:{see}\:{that} \\ $$$${x}_{\mathrm{0}} =\frac{\mathrm{3}}{\mathrm{4}}\:\:,\:{y}_{\mathrm{0}} =−\mathrm{1} \\ $$$${y}−\mathrm{3}=\frac{\mathrm{3}−\left(−\mathrm{1}\right)}{\left(\mathrm{2}−\frac{\mathrm{3}}{\mathrm{4}}\right)}\:\left({x}−\mathrm{2}\right) \\ $$$${y}−\mathrm{3}=\frac{\mathrm{16}}{\mathrm{5}}\left({x}−\mathrm{2}\right) \\ $$$$\mathrm{5}{y}−\mathrm{15}=\mathrm{16}{x}−\mathrm{32} \\ $$$$\mathrm{5}\boldsymbol{{y}}=\mathrm{16}\boldsymbol{{x}}−\mathrm{17}\:. \\ $$
Commented by *D¬ B£$T* last updated on 20/Oct/17
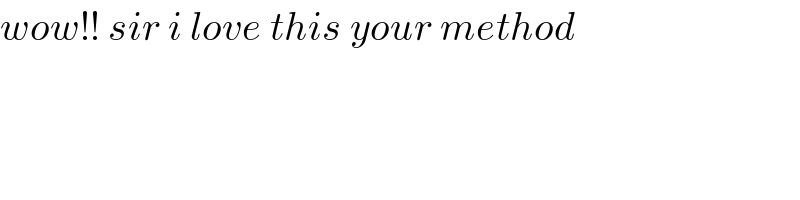
$${wow}!!\:{sir}\:{i}\:{love}\:{this}\:{your}\:{method} \\ $$
Commented by *D¬ B£$T* last updated on 20/Oct/17
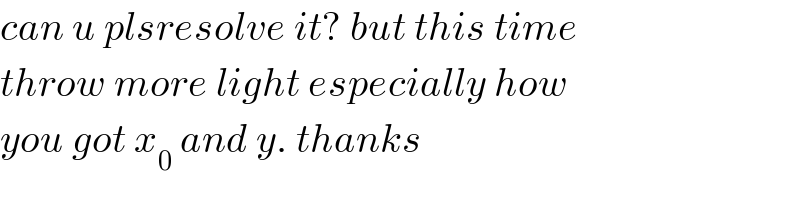
$${can}\:{u}\:{plsresolve}\:{it}?\:{but}\:{this}\:{time} \\ $$$${throw}\:{more}\:{light}\:{especially}\:{how} \\ $$$${you}\:{got}\:{x}_{\mathrm{0}} \:{and}\:{y}.\:{thanks} \\ $$
Commented by *D¬ B£$T* last updated on 20/Oct/17

$${thanks}\:{sir} \\ $$
