Question Number 162074 by naka3546 last updated on 26/Dec/21
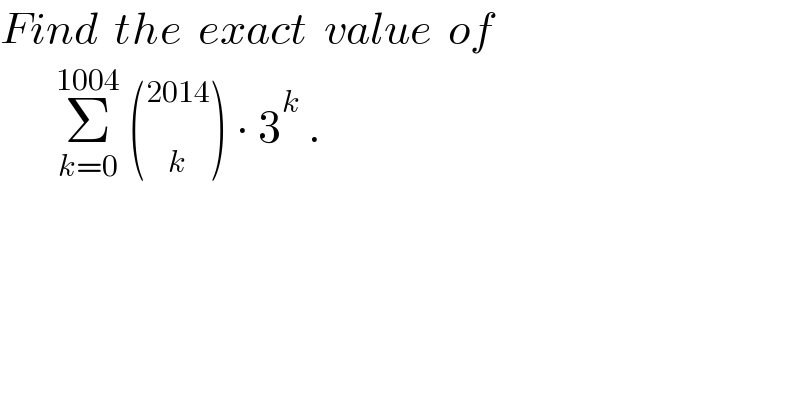
$${Find}\:\:{the}\:\:{exact}\:\:{value}\:\:{of} \\ $$$$\:\:\:\:\:\:\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{1004}} {\sum}}\:\left(\underset{{k}} {\overset{\mathrm{2014}} {\:}}\right)\:\centerdot\:\mathrm{3}^{{k}} \:. \\ $$
Answered by Rasheed.Sindhi last updated on 26/Dec/21

$$\left({a}+{b}\right)^{{n}} =\overset{{n}} {\underset{{k}=\mathrm{0}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{a}^{{n}−{k}} {b}^{{k}} \\ $$$${Let}\:{a}=\mathrm{1}\:,\:{b}=\mathrm{3}\:\&\:{n}=\mathrm{2014} \\ $$$${S}\left(\mathrm{2015}\right)=\left(\mathrm{1}+\mathrm{3}\right)^{\mathrm{2014}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2014}} {\sum}}\begin{pmatrix}{\mathrm{2014}}\\{\:\:\:\:{k}}\end{pmatrix}.\mathrm{3}^{{k}} =\mathrm{4}^{\mathrm{2014}} ….\left({i}\right) \\ $$$${We}'{ve}\:{to}\:{determine}\:{first}\:\mathrm{1005}\:{terms}\left({sum}\right) \\ $$$${i}-{e}\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{1004}} {\sum}}\:\left(\underset{{k}} {\overset{\mathrm{2014}} {\:}}\right)\:\centerdot\:\mathrm{3}^{{k}} \: \\ $$$${S}\left(\mathrm{1to2015}\right)=\underset{\mathrm{S}_{\mathrm{1}} } {\underbrace{\left\{\mathrm{t}_{\mathrm{1}} +\mathrm{t}_{\mathrm{2}} +…\mathrm{t}_{\mathrm{1007}} +\frac{\mathrm{t}_{\mathrm{1008}} }{\mathrm{2}}\right\}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{S}_{\mathrm{2}} } {\underbrace{\left\{\frac{\mathrm{t}_{\mathrm{1008}} }{\mathrm{2}}+\mathrm{t}_{\mathrm{1009}} +\mathrm{t}_{\mathrm{1010}} +…+\mathrm{t}_{\mathrm{2015}} \right\}}} \\ $$$$\:\because{Here}\:{S}_{\mathrm{1}} ={S}_{\mathrm{2}} \:\:\:\:\therefore\:{S}_{\mathrm{1}} ={S}/\mathrm{2}=\mathrm{4}^{\mathrm{2014}} /\mathrm{2} \\ $$$$\Rightarrow{S}_{\mathrm{1}} =\mathrm{4}^{\mathrm{2013}} \\ $$$$\therefore\:{S}\left(\mathrm{1to1005}\right)={S}_{\mathrm{1}} −\left(\mathrm{t}_{\mathrm{1006}} +\mathrm{t}_{\mathrm{1007}} +\frac{\mathrm{t}_{\mathrm{1008}} }{\mathrm{2}}\right) \\ $$$$=\mathrm{4}^{\mathrm{2013}} −\left(\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1005}}\end{pmatrix}.\mathrm{3}^{\mathrm{1005}} +\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1006}}\end{pmatrix}.\mathrm{3}^{\mathrm{1006}} +\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix}.\mathrm{3}^{\mathrm{1007}} \right) \\ $$$$=\mathrm{4}^{\mathrm{2013}} −\mathrm{3}^{\mathrm{1005}} \left(\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1005}}\end{pmatrix}+\mathrm{3}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1006}}\end{pmatrix}+\frac{\mathrm{9}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix}\right) \\ $$
Commented by naka3546 last updated on 26/Dec/21
$${Thank}\:\:{you},\:\:{sir}. \\ $$
