Menu Close

find-the-first-4-terms-in-the-maclaurin-series-expansion-for-ln-1-3x-hence-show-that-if-x-2-and-higher-powers-of-x-are-negleted-then-1-3x-3-x-e-6-1-9x-

Tinku Tara 0 Comments
Pin




Question Number 83202 by Rio Michael last updated on 28/Feb/20
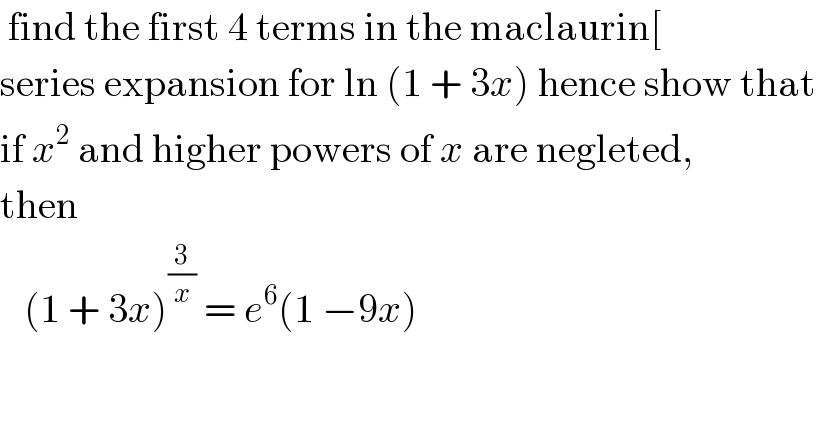
find the first 4 terms in the maclaurin[ series expansion for ln (1 + 3x) hence show that if x^2 and higher powers of x are negleted, then (1 + 3x)^(3/x) = e^6 (1 −9x)
$$\:\mathrm{find}\:\mathrm{the}\:\mathrm{first}\:\mathrm{4}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{maclaurin}\left[\right. \\ $$$$\mathrm{series}\:\mathrm{expansion}\:\mathrm{for}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)\:\mathrm{hence}\:\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{if}\:{x}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{higher}\:\mathrm{powers}\:\mathrm{of}\:{x}\:\mathrm{are}\:\mathrm{negleted}, \\ $$$$\mathrm{then}\: \\ $$$$\:\:\:\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}} \:=\:{e}^{\mathrm{6}} \left(\mathrm{1}\:−\mathrm{9}{x}\right) \\ $$
Commented by mr W last updated on 28/Feb/20
i think the question is wrong. please check sir! f(x)=(1 + 3x)^(3/x) g(x) = e^6 (1 −9x) f(0)≠g(0) f′(0)≠g′(0) ⇒f(x)≈g(x) is not true! i think correct is (1 + 3x)^(3/x) ≈e^9 (1 −((27)/2)x)
$${i}\:{think}\:{the}\:{question}\:{is}\:{wrong}.\:{please} \\ $$$${check}\:{sir}! \\ $$$${f}\left({x}\right)=\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}} \\ $$$${g}\left({x}\right)\:=\:{e}^{\mathrm{6}} \left(\mathrm{1}\:−\mathrm{9}{x}\right) \\ $$$${f}\left(\mathrm{0}\right)\neq{g}\left(\mathrm{0}\right) \\ $$$${f}'\left(\mathrm{0}\right)\neq{g}'\left(\mathrm{0}\right) \\ $$$$\Rightarrow{f}\left({x}\right)\approx{g}\left({x}\right)\:{is}\:{not}\:{true}! \\ $$$$ \\ $$$${i}\:{think}\:{correct}\:{is} \\ $$$$\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}} \:\approx{e}^{\mathrm{9}} \left(\mathrm{1}\:−\frac{\mathrm{27}}{\mathrm{2}}{x}\right) \\ $$
Commented by Rio Michael last updated on 28/Feb/20
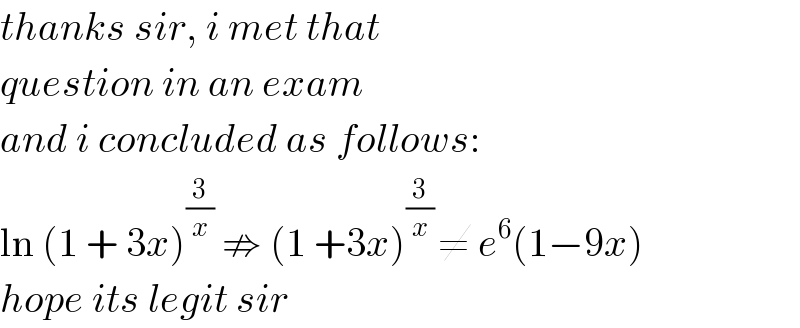
thanks sir, i met that question in an exam and i concluded as follows: ln (1 + 3x)^(3/x) ⇏ (1 +3x)^((3/x) ) ≠ e^6 (1−9x) hope its legit sir
$${thanks}\:{sir},\:{i}\:{met}\:{that}\: \\ $$$${question}\:{in}\:{an}\:{exam}\: \\ $$$${and}\:{i}\:{concluded}\:{as}\:{follows}: \\ $$$$\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}} \:\nRightarrow\:\left(\mathrm{1}\:+\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}\:} \neq\:{e}^{\mathrm{6}} \left(\mathrm{1}−\mathrm{9}{x}\right) \\ $$$${hope}\:{its}\:{legit}\:{sir} \\ $$
Commented by mr W last updated on 28/Feb/20
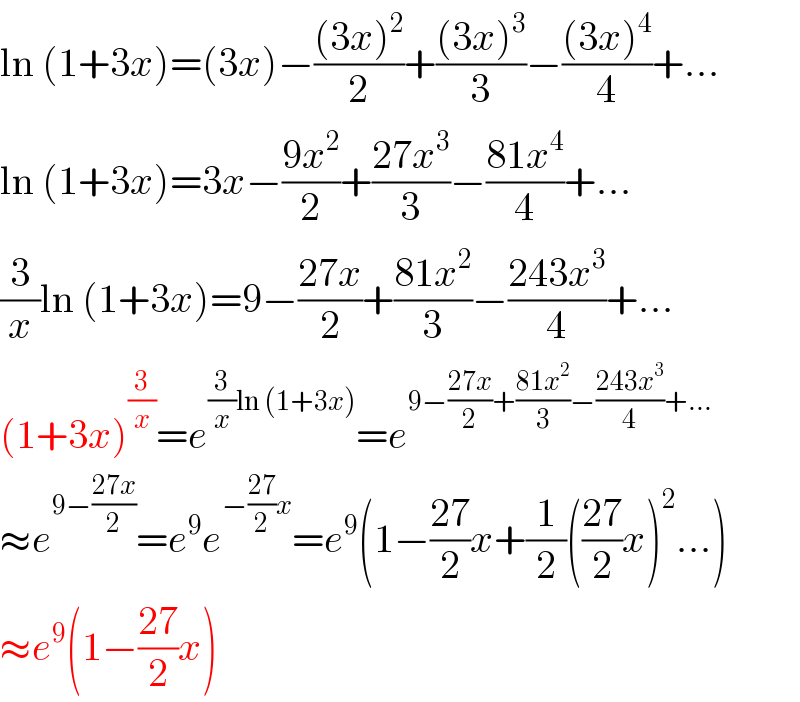
ln (1+3x)=(3x)−(((3x)^2 )/2)+(((3x)^3 )/3)−(((3x)^4 )/4)+... ln (1+3x)=3x−((9x^2 )/2)+((27x^3 )/3)−((81x^4 )/4)+... (3/x)ln (1+3x)=9−((27x)/2)+((81x^2 )/3)−((243x^3 )/4)+... (1+3x)^(3/x) =e^((3/x)ln (1+3x)) =e^(9−((27x)/2)+((81x^2 )/3)−((243x^3 )/4)+...) ≈e^(9−((27x)/2)) =e^9 e^(−((27)/2)x) =e^9 (1−((27)/2)x+(1/2)(((27)/2)x)^2 ...) ≈e^9 (1−((27)/2)x)
$$\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}\right)=\left(\mathrm{3}{x}\right)−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{4}} }{\mathrm{4}}+… \\ $$$$\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}\right)=\mathrm{3}{x}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{27}{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{81}{x}^{\mathrm{4}} }{\mathrm{4}}+… \\ $$$$\frac{\mathrm{3}}{{x}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}\right)=\mathrm{9}−\frac{\mathrm{27}{x}}{\mathrm{2}}+\frac{\mathrm{81}{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{243}{x}^{\mathrm{3}} }{\mathrm{4}}+… \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)^{\frac{\mathrm{3}}{{x}}} ={e}^{\frac{\mathrm{3}}{{x}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{3}{x}\right)} ={e}^{\mathrm{9}−\frac{\mathrm{27}{x}}{\mathrm{2}}+\frac{\mathrm{81}{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{243}{x}^{\mathrm{3}} }{\mathrm{4}}+…} \\ $$$$\approx{e}^{\mathrm{9}−\frac{\mathrm{27}{x}}{\mathrm{2}}} ={e}^{\mathrm{9}} {e}^{−\frac{\mathrm{27}}{\mathrm{2}}{x}} ={e}^{\mathrm{9}} \left(\mathrm{1}−\frac{\mathrm{27}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{27}}{\mathrm{2}}{x}\right)^{\mathrm{2}} …\right) \\ $$$$\approx{e}^{\mathrm{9}} \left(\mathrm{1}−\frac{\mathrm{27}}{\mathrm{2}}{x}\right) \\ $$
Commented by Rio Michael last updated on 28/Feb/20
thanks sir
$${thanks}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *