Question Number 170199 by Mastermind last updated on 18/May/22

$${Find}\:{the}\:{first}\:{four}\:{terms}\:{of}\:{the}\:{series} \\ $$$${for}\:{e}^{{x}} {sinhx} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by floor(10²Eta[1]) last updated on 18/May/22
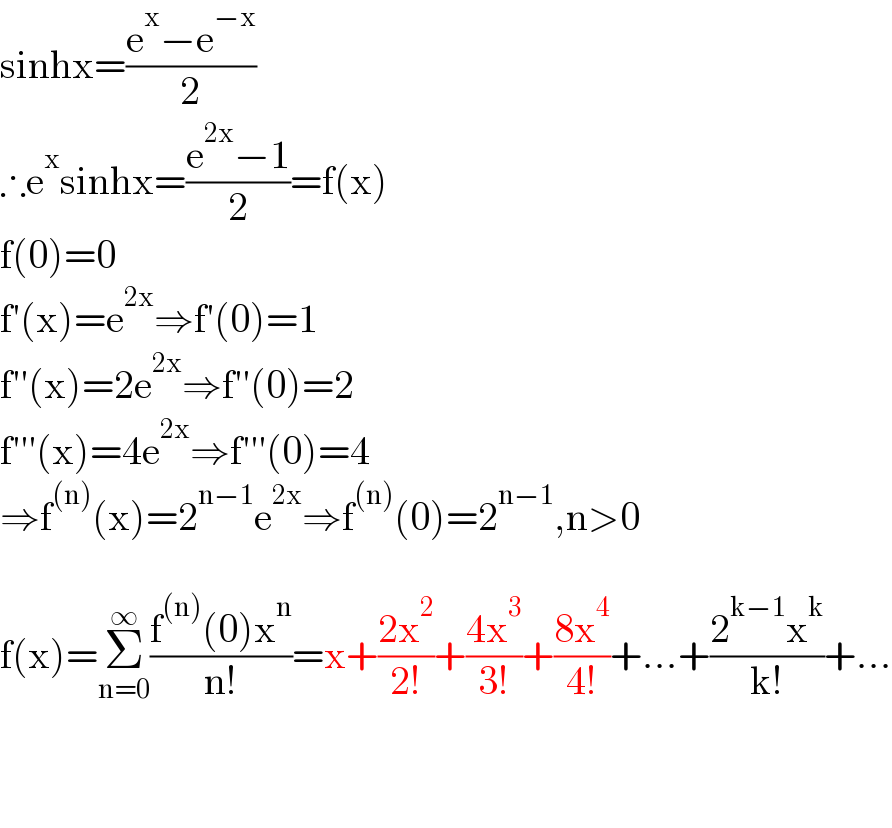
$$\mathrm{sinhx}=\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}} \\ $$$$\therefore\mathrm{e}^{\mathrm{x}} \mathrm{sinhx}=\frac{\mathrm{e}^{\mathrm{2x}} −\mathrm{1}}{\mathrm{2}}=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{2x}} \Rightarrow\mathrm{f}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{f}''\left(\mathrm{x}\right)=\mathrm{2e}^{\mathrm{2x}} \Rightarrow\mathrm{f}''\left(\mathrm{0}\right)=\mathrm{2} \\ $$$$\mathrm{f}'''\left(\mathrm{x}\right)=\mathrm{4e}^{\mathrm{2x}} \Rightarrow\mathrm{f}'''\left(\mathrm{0}\right)=\mathrm{4} \\ $$$$\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\mathrm{2}^{\mathrm{n}−\mathrm{1}} \mathrm{e}^{\mathrm{2x}} \Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)=\mathrm{2}^{\mathrm{n}−\mathrm{1}} ,\mathrm{n}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\mathrm{x}^{\mathrm{n}} }{\mathrm{n}!}=\mathrm{x}+\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{4x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{8x}^{\mathrm{4}} }{\mathrm{4}!}+…+\frac{\mathrm{2}^{\mathrm{k}−\mathrm{1}} \mathrm{x}^{\mathrm{k}} }{\mathrm{k}!}+… \\ $$$$ \\ $$$$ \\ $$
Commented by Mastermind last updated on 19/May/22

$${thanks} \\ $$
