Question Number 154896 by maged last updated on 22/Sep/21
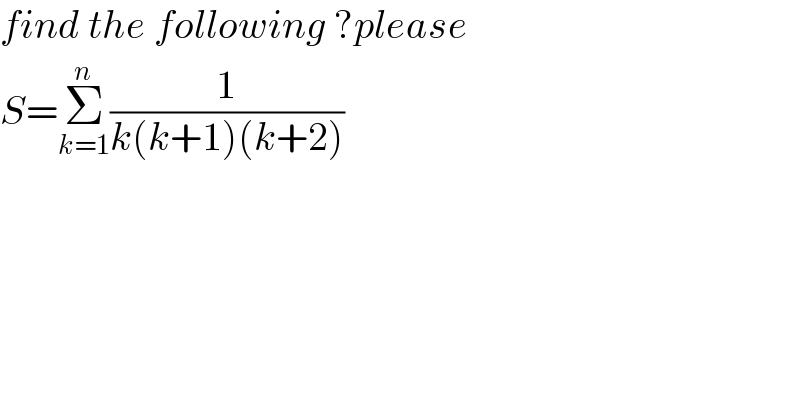
$${find}\:{the}\:{following}\:?{please} \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$
Commented by benhamimed last updated on 23/Sep/21
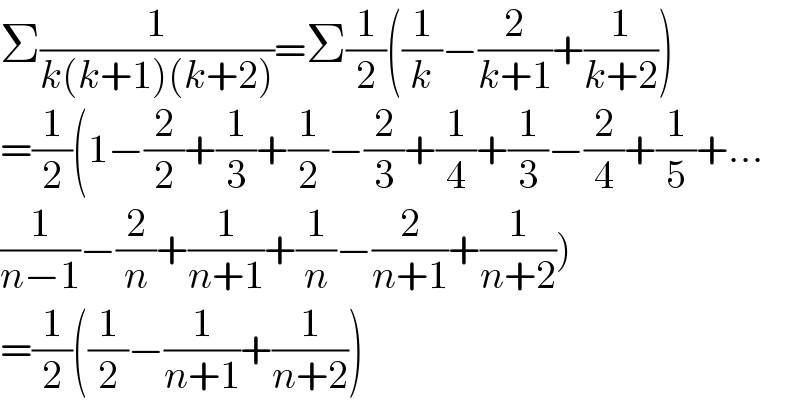
$$\Sigma\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}=\Sigma\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{2}}{{k}+\mathrm{1}}+\frac{\mathrm{1}}{{k}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+…\right. \\ $$$$\left.\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{2}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{2}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$
Commented by maged last updated on 23/Sep/21

$${Thank}\:{you} \\ $$
