Menu Close

Find-the-fourier-series-of-f-x-x-from-0-lt-x-lt-pi-

Tinku Tara 0 Comments
Pin




Question Number 17625 by tawa tawa last updated on 08/Jul/17
Find the fourier series of : f(x) = x, from 0 < x < π
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{fourier}\:\mathrm{series}\:\mathrm{of}\::\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x},\:\:\mathrm{from}\:\:\:\mathrm{0}\:<\:\mathrm{x}\:<\:\pi \\ $$
Commented by tawa tawa last updated on 08/Jul/17
please help with this.
$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}. \\ $$
Answered by alex041103 last updated on 09/Jul/17
(π/2)−Σ_(n=1) ^∞ ((sin(2nx))/n) = f(x) = x when x∈(0, π)
$$\frac{\pi}{\mathrm{2}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{nx}\right)}{{n}}\:=\:{f}\left({x}\right)\:=\:{x}\:{when}\:{x}\in\left(\mathrm{0},\:\pi\right) \\ $$
Commented by tawa tawa last updated on 09/Jul/17
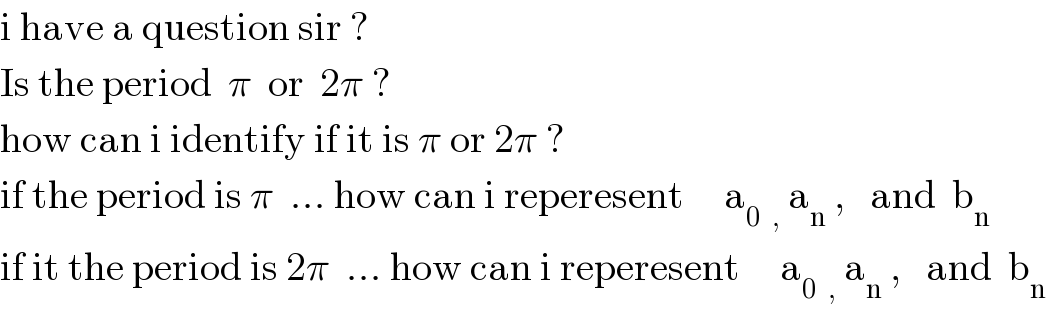
i have a question sir ? Is the period π or 2π ? how can i identify if it is π or 2π ? if the period is π ... how can i reperesent a_(0 , ) a_n , and b_n if it the period is 2π ... how can i reperesent a_(0 , ) a_n , and b_n
$$\mathrm{i}\:\mathrm{have}\:\mathrm{a}\:\mathrm{question}\:\mathrm{sir}\:? \\ $$$$\mathrm{Is}\:\mathrm{the}\:\mathrm{period}\:\:\pi\:\:\mathrm{or}\:\:\mathrm{2}\pi\:? \\ $$$$\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{identify}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\pi\:\mathrm{or}\:\mathrm{2}\pi\:? \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{period}\:\mathrm{is}\:\pi\:\:…\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{reperesent}\:\:\:\:\:\mathrm{a}_{\mathrm{0}\:\:\:,\:\:} \mathrm{a}_{\mathrm{n}} \:,\:\:\:\mathrm{and}\:\:\mathrm{b}_{\mathrm{n}} \\ $$$$\mathrm{if}\:\mathrm{it}\:\mathrm{the}\:\mathrm{period}\:\mathrm{is}\:\mathrm{2}\pi\:\:…\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{reperesent}\:\:\:\:\:\mathrm{a}_{\mathrm{0}\:\:\:,\:\:} \mathrm{a}_{\mathrm{n}} \:,\:\:\:\mathrm{and}\:\:\mathrm{b}_{\mathrm{n}} \\ $$
Commented by alex041103 last updated on 09/Jul/17
It′s easy to prove that if f(x)=c+Σ_(n=1) ^∞ [a_n cos(((2πnx)/T)) + b_n sin(((2πnx)/T))] then c=(1/T)∫_0 ^T f(x) dx a_n =(2/T)∫_0 ^T f(x)cos(((2πnx)/T)) dx b_b =(2/T)∫_0 ^T f(x)sin(((2πnx)/T)) dx In the case of f(x)=x we will set the period T=π ⇒c=(π/2) , a_n =0 , b_n =−(1/n) ⇒x∈(0, π), f(x)=(π/2) − Σ_(n=1) ^∞ ((sin(2nx))/n)
$$ \\ $$$${It}'{s}\:{easy}\:{to}\:{prove}\:{that}\:{if} \\ $$$${f}\left({x}\right)={c}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[{a}_{{n}} {cos}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:+\:{b}_{{n}} {sin}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\right] \\ $$$${then} \\ $$$${c}=\frac{\mathrm{1}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right)\:{dx} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right){cos}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:{dx} \\ $$$${b}_{{b}} =\frac{\mathrm{2}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right){sin}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:{dx} \\ $$$$ \\ $$$${In}\:{the}\:{case}\:{of}\:{f}\left({x}\right)={x}\:{we}\:{will}\:{set}\:{the}\:{period}\: \\ $$$${T}=\pi \\ $$$$\Rightarrow{c}=\frac{\pi}{\mathrm{2}}\:,\:{a}_{{n}} =\mathrm{0}\:,\:{b}_{{n}} =−\frac{\mathrm{1}}{{n}} \\ $$$$\Rightarrow{x}\in\left(\mathrm{0},\:\pi\right),\:{f}\left({x}\right)=\frac{\pi}{\mathrm{2}}\:−\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$
Commented by tawa tawa last updated on 09/Jul/17
That means for period 2π a_0 = (1/π) ∫_( 0) ^( 2π) f(x) a_n = (1/π) ∫_( 0) ^( 2π) f(x)cos(nx) b_n = (1/π) ∫_( 0) ^( 2π) f(x)sin(nx) Again, That means for period π a_0 = (2/π) ∫_( 0) ^( π) f(x) a_n = (2/π) ∫_( 0) ^( π) f(x)cos(nx) b_n = (2/π) ∫_( 0) ^( π) f(x)sin(nx) ??????????????
$$\mathrm{That}\:\mathrm{means}\:\mathrm{for}\:\mathrm{period}\:\:\mathrm{2}\pi \\ $$$$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{nx}\right) \\ $$$$\mathrm{Again}, \\ $$$$\mathrm{That}\:\mathrm{means}\:\mathrm{for}\:\mathrm{period}\:\:\pi \\ $$$$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{nx}\right) \\ $$$$?????????????? \\ $$
Commented by alex041103 last updated on 09/Jul/17
No. For period of π we have: b_n = (2/π) ∫_( 0) ^( π) f(x)sin(((2π)/π)nx)dx=(2/π)∫_0 ^π f(x)sin(2nx) dx a_n = (2/π) ∫_( 0) ^( π) f(x)cos(((2π)/π)nx) dx=(2/π)∫_0 ^π f(x)cos(2nx) dx a_0 = (2/π) ∫_( 0) ^( π) f(x) dx And in fact if we use T=2π(the period is 2π) we are going to get fourier seriesfor f(x)=x for x∈[0, 2π]
$${No}. \\ $$$${For}\:{period}\:{of}\:\pi\:{we}\:{have}: \\ $$$$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\pi}\mathrm{nx}\right){dx}=\frac{\mathrm{2}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){sin}\left(\mathrm{2}{nx}\right)\:{dx} \\ $$$$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\pi}\mathrm{nx}\right)\:{dx}=\frac{\mathrm{2}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){cos}\left(\mathrm{2}{nx}\right)\:{dx} \\ $$$$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\:{dx} \\ $$$${And}\:{in}\:{fact}\:{if}\:{we}\:{use}\:{T}=\mathrm{2}\pi\left({the}\:{period}\:{is}\:\mathrm{2}\pi\right)\: \\ $$$${we}\:{are}\:{going}\:{to}\:{get}\:{fourier}\:{seriesfor} \\ $$$${f}\left({x}\right)={x}\:{for}\:{x}\in\left[\mathrm{0},\:\mathrm{2}\pi\right] \\ $$
Commented by tawa tawa last updated on 09/Jul/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by alex041103 last updated on 10/Jul/17
Commented by alex041103 last updated on 10/Jul/17
Blue→T=2π,i.e. for 0<x<2π x=π−2Σ_(n=1) ^∞ ((sin(nx))/n) Red→T=π,i.e. for 0<x<π x=(π/2)−Σ_(n=1) ^∞ ((sin(2nx))/n)
$$\mathrm{Blue}\rightarrow\mathrm{T}=\mathrm{2}\pi,\mathrm{i}.\mathrm{e}.\:\mathrm{for}\:\mathrm{0}<\mathrm{x}<\mathrm{2}\pi \\ $$$$\mathrm{x}=\pi−\mathrm{2}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{nx}\right)}{\mathrm{n}} \\ $$$$\mathrm{Red}\rightarrow\mathrm{T}=\pi,\mathrm{i}.\mathrm{e}.\:\mathrm{for}\:\mathrm{0}<\mathrm{x}<\pi \\ $$$$\mathrm{x}=\frac{\pi}{\mathrm{2}}−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2nx}\right)}{\mathrm{n}} \\ $$
Commented by tawa tawa last updated on 10/Jul/17
i really appreciate your effort sir. God bless you.
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *