Question Number 55301 by Otchere Abdullai last updated on 20/Feb/19
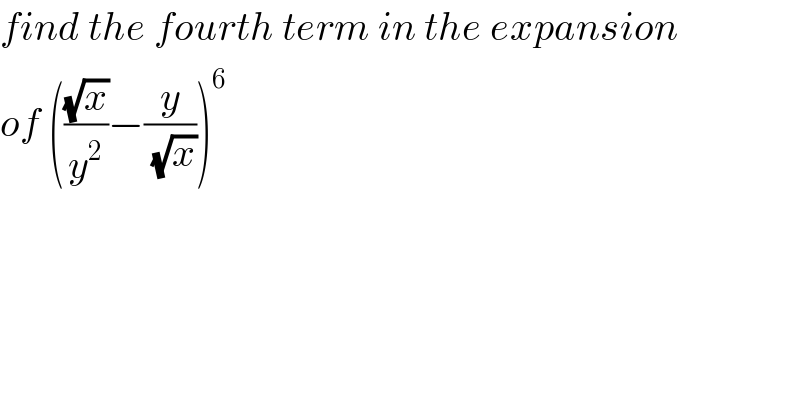
$${find}\:{the}\:{fourth}\:{term}\:{in}\:{the}\:{expansion} \\ $$$${of}\:\left(\frac{\sqrt{{x}}}{{y}^{\mathrm{2}} }−\frac{{y}}{\:\sqrt{{x}}}\right)^{\mathrm{6}} \\ $$
Commented by mr W last updated on 21/Feb/19
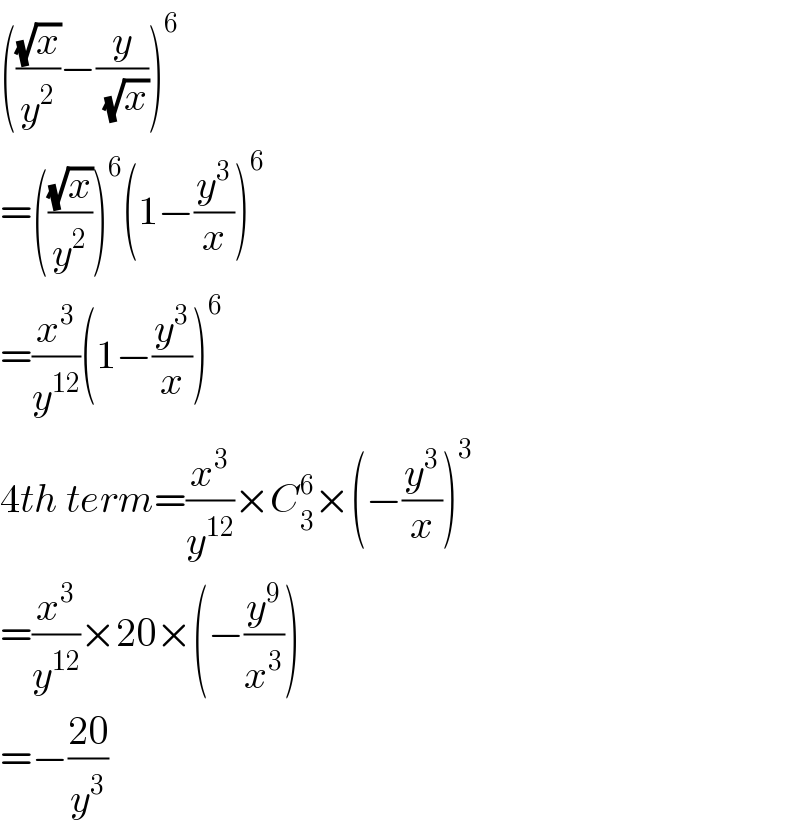
$$\left(\frac{\sqrt{{x}}}{{y}^{\mathrm{2}} }−\frac{{y}}{\:\sqrt{{x}}}\right)^{\mathrm{6}} \\ $$$$=\left(\frac{\sqrt{{x}}}{{y}^{\mathrm{2}} }\right)^{\mathrm{6}} \left(\mathrm{1}−\frac{{y}^{\mathrm{3}} }{{x}}\right)^{\mathrm{6}} \\ $$$$=\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{12}} }\left(\mathrm{1}−\frac{{y}^{\mathrm{3}} }{{x}}\right)^{\mathrm{6}} \\ $$$$\mathrm{4}{th}\:{term}=\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{12}} }×{C}_{\mathrm{3}} ^{\mathrm{6}} ×\left(−\frac{{y}^{\mathrm{3}} }{{x}}\right)^{\mathrm{3}} \\ $$$$=\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{12}} }×\mathrm{20}×\left(−\frac{{y}^{\mathrm{9}} }{{x}^{\mathrm{3}} }\right) \\ $$$$=−\frac{\mathrm{20}}{{y}^{\mathrm{3}} } \\ $$
Commented by Otchere Abdullai last updated on 21/Feb/19
$${God}\:{bless}\:{you}\:{Prof}\:{W} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Feb/19

$${r}+\mathrm{1}\:{th}\:{term}\:\rightarrow{nc}_{{r}} \left({a}\right)^{{n}−{r}} \left({b}\right)^{{r}} \\ $$$${so}\:\mathrm{4}{th}\:{term}\rightarrow\mathrm{6}{c}_{\mathrm{3}} \left(\frac{\sqrt{{x}}}{{y}^{\mathrm{2}} }\right)^{\mathrm{6}−\mathrm{3}} \left(\frac{−{y}}{\:\sqrt{{x}}}\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{6}!}{\mathrm{3}!×\mathrm{3}!}\frac{\left({x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\left({y}\right)^{\mathrm{6}} }×\left(−\mathrm{1}\right)×\frac{{y}^{\mathrm{3}} }{\left({x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{−\mathrm{20}}{{y}^{\mathrm{3}} } \\ $$
Commented by Otchere Abdullai last updated on 21/Feb/19
$${thank}\:{you}\:{prof}\:{Tanmay} \\ $$
