Find-the-function-whose-first-derivative-is-8-5-x-2-1-3-the-initial-conditions-f-8-20-

Question Number 50161 by cesar.marval.larez@gmail.com last updated on 14/Dec/18

F i n d t h e f u n c t i o n w h o s e f i r s t

d e r i v a t i v e i s 8 - \frac{5}{\sqrt[3]{x^{2}}} t h e i n i t i a l

c o n d i t i o n s f (8) = - 20

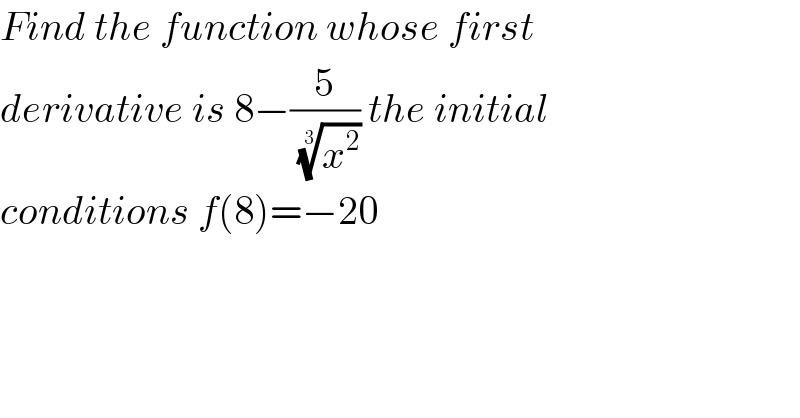
Answered by afachri last updated on 14/Dec/18

F (x) = \int f^{'} (x) d x

= \int 8 - 5 x^{- \frac{2}{3}} d x

= 8 x - (\frac{5}{(- \frac{2}{3} + 1)}) x^{- \frac{2}{3} + 1} + C

= 8 x - 15 x^{\frac{1}{3}} + C

to find C :

F (8) = - 20

8 (8) - 15 {(8)}^{\frac{1}{3}} + C = - 20

64 - 30 + C = - 20

C = - 54

So : F (x) = 8 x - 15 x^{\frac{1}{3}} - 54

Commented by cesar.marval.larez@gmail.com last updated on 14/Dec/18

w o w f r i e n d m y r e s p e c t i w i l l t h e o t h e r s

Commented by afachri last updated on 14/Dec/18

{it}^{'} s been our pleasure

Facebook Tweet Pin