Menu Close

find-the-general-formula-0-pi-2-tan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 97928 by  M±th+et+s last updated on 10/Jun/20
find the general formula ∫_0 ^(π/2) tan^α (x) dx
$${find}\:{the}\:{general}\:{formula} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {tan}^{\alpha} \left({x}\right)\:{dx} \\ $$
Answered by abdomathmax last updated on 10/Jun/20
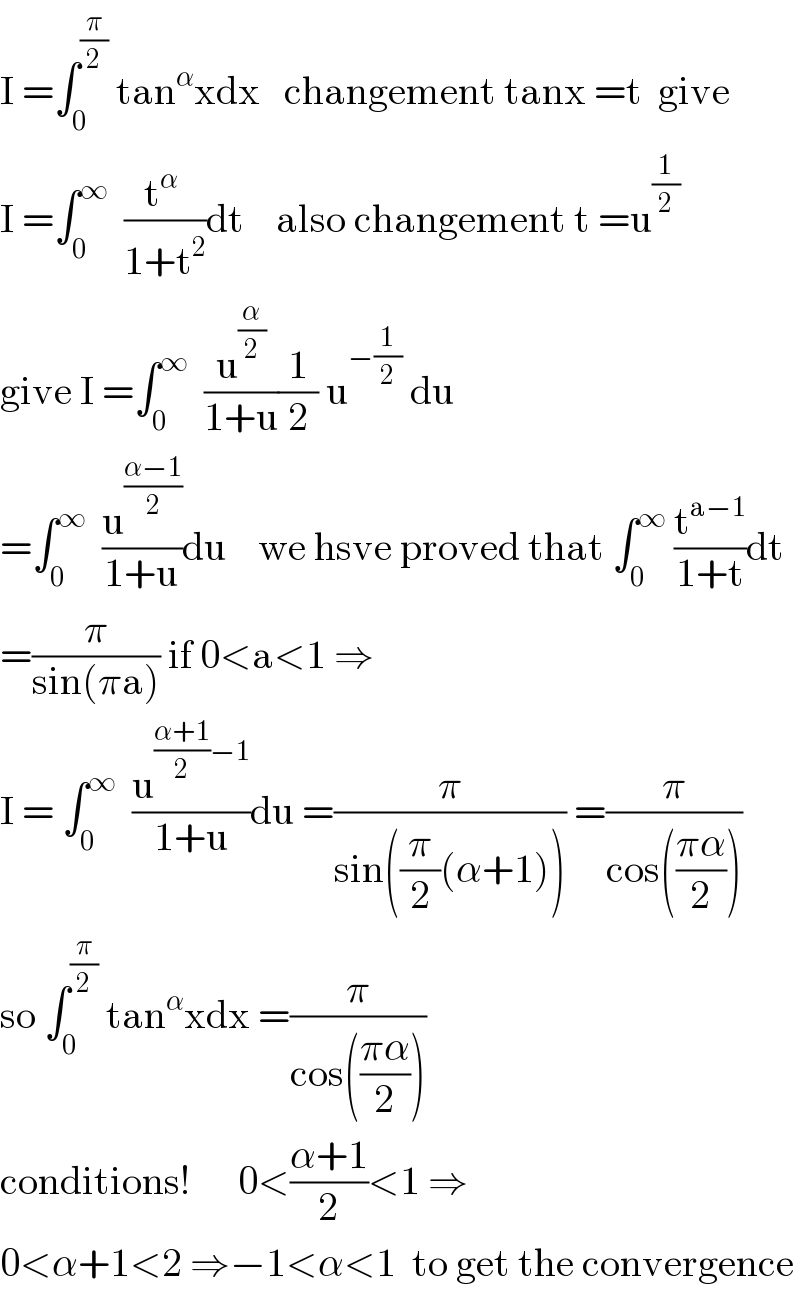
I =∫_0 ^(π/2) tan^α xdx changement tanx =t give I =∫_0 ^∞ ((t^α )/(1+t^2 ))dt also changement t =u^(1/2) give I =∫_0 ^∞ (u^(α/2) /(1+u))(1/2) u^(−(1/2)) du =∫_0 ^∞ (u^((α−1)/2) /(1+u))du we hsve proved that ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) if 0<a<1 ⇒ I = ∫_0 ^∞ (u^(((α+1)/2)−1) /(1+u))du =(π/(sin((π/2)(α+1)))) =(π/(cos(((πα)/2)))) so ∫_0 ^(π/2) tan^α xdx =(π/(cos(((πα)/2)))) conditions! 0<((α+1)/2)<1 ⇒ 0<α+1<2 ⇒−1<α<1 to get the convergence
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{tan}^{\alpha} \mathrm{xdx}\:\:\:\mathrm{changement}\:\mathrm{tanx}\:=\mathrm{t}\:\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\alpha} \:}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:\:\:\mathrm{also}\:\mathrm{changement}\:\mathrm{t}\:=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{give}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\alpha}{\mathrm{2}}} }{\mathrm{1}+\mathrm{u}}\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\alpha−\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+\mathrm{u}}\mathrm{du}\:\:\:\:\mathrm{we}\:\mathrm{hsve}\:\mathrm{proved}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\mathrm{if}\:\mathrm{0}<\mathrm{a}<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\alpha+\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}+\mathrm{u}}\mathrm{du}\:=\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\left(\alpha+\mathrm{1}\right)\right)}\:=\frac{\pi}{\mathrm{cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)} \\ $$$$\mathrm{so}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{tan}^{\alpha} \mathrm{xdx}\:=\frac{\pi}{\mathrm{cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)} \\ $$$$\mathrm{conditions}!\:\:\:\:\:\:\mathrm{0}<\frac{\alpha+\mathrm{1}}{\mathrm{2}}<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{0}<\alpha+\mathrm{1}<\mathrm{2}\:\Rightarrow−\mathrm{1}<\alpha<\mathrm{1}\:\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{convergence} \\ $$
Commented by  M±th+et+s last updated on 11/Jun/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 11/Jun/20
you are welcome .
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *