Question Number 147621 by mathdanisur last updated on 22/Jul/21
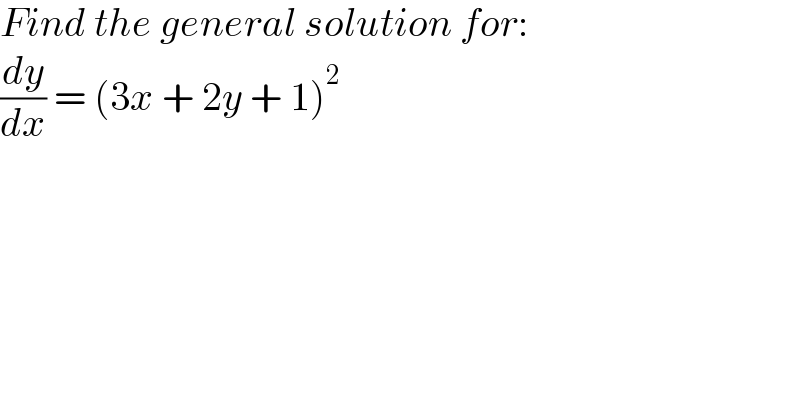
$${Find}\:{the}\:{general}\:{solution}\:{for}: \\ $$$$\frac{{dy}}{{dx}}\:=\:\left(\mathrm{3}{x}\:+\:\mathrm{2}{y}\:+\:\mathrm{1}\right)^{\mathrm{2}} \\ $$
Answered by gsk2684 last updated on 22/Jul/21
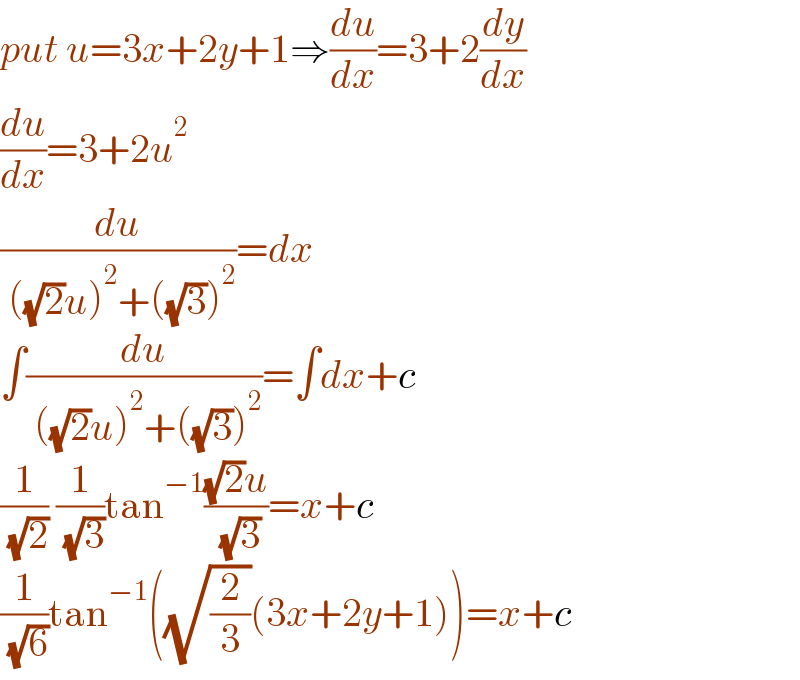
$${put}\:{u}=\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{1}\Rightarrow\frac{{du}}{{dx}}=\mathrm{3}+\mathrm{2}\frac{{dy}}{{dx}} \\ $$$$\frac{{du}}{{dx}}=\mathrm{3}+\mathrm{2}{u}^{\mathrm{2}} \\ $$$$\frac{{du}}{\:\left(\sqrt{\mathrm{2}}{u}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }={dx} \\ $$$$\int\frac{{du}}{\:\left(\sqrt{\mathrm{2}}{u}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\int{dx}+{c} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}{u}}{\:\sqrt{\mathrm{3}}}={x}+{c} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\left(\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{1}\right)\right)={x}+{c} \\ $$
Commented by puissant last updated on 22/Jul/21

$$\mathrm{jolie}\:\mathrm{prof}..\:\mathrm{Nice}\: \\ $$
Commented by mathdanisur last updated on 22/Jul/21
$${Thank}\:{you}\:{Sir}\:{cool} \\ $$
