Question Number 178694 by peter frank last updated on 20/Oct/22
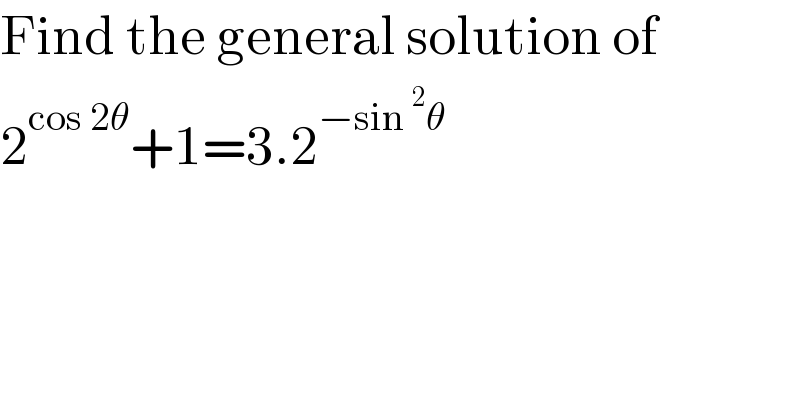
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of} \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}\theta} +\mathrm{1}=\mathrm{3}.\mathrm{2}^{−\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$
Answered by Frix last updated on 20/Oct/22
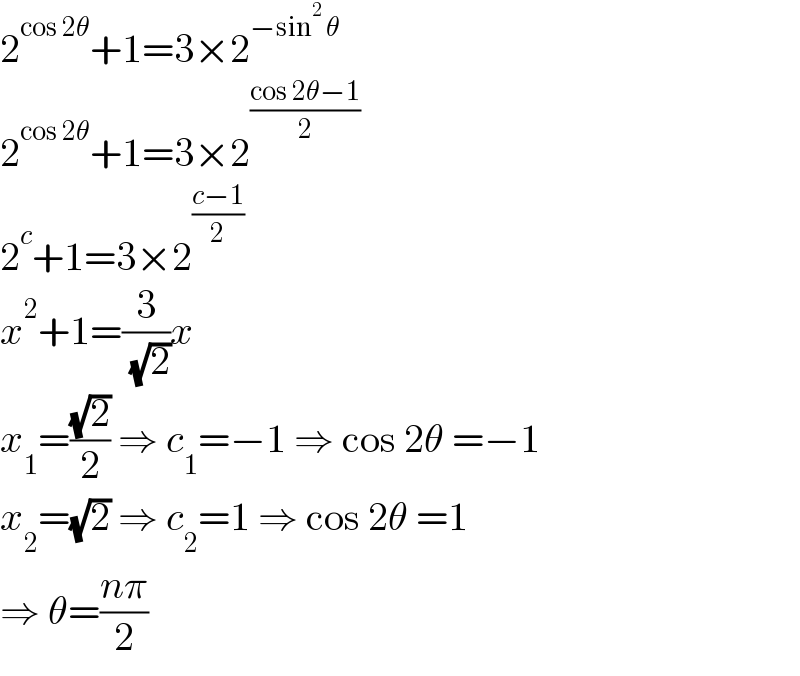
$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}\theta} +\mathrm{1}=\mathrm{3}×\mathrm{2}^{−\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\mathrm{2}^{\mathrm{cos}\:\mathrm{2}\theta} +\mathrm{1}=\mathrm{3}×\mathrm{2}^{\frac{\mathrm{cos}\:\mathrm{2}\theta−\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}^{{c}} +\mathrm{1}=\mathrm{3}×\mathrm{2}^{\frac{{c}−\mathrm{1}}{\mathrm{2}}} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}{x} \\ $$$${x}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\:{c}_{\mathrm{1}} =−\mathrm{1}\:\Rightarrow\:\mathrm{cos}\:\mathrm{2}\theta\:=−\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\sqrt{\mathrm{2}}\:\Rightarrow\:{c}_{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:\mathrm{cos}\:\mathrm{2}\theta\:=\mathrm{1} \\ $$$$\Rightarrow\:\theta=\frac{{n}\pi}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 20/Oct/22
Welldone sir MJS��������
Commented by Rasheed.Sindhi last updated on 21/Oct/22

$${Your}\:{sense}\:{of}\:{guessing}\:{is}\:{powerful}. \\ $$$${I}\:{remember}\:{that}\:{you}\:{had}\:{once}\:{guessed} \\ $$$${correctly}\:{for}\:“{Her}-{majesty}''\:{to}\:{be} \\ $$$${MJS}\:\boldsymbol{{sir}}!\:{I}\:{think}\:{you}'{re}\:{also}\:{correct} \\ $$$${this}\:{time}! \\ $$
Commented by Ar Brandon last updated on 21/Oct/22
������
Commented by ARUNG_Brandon_MBU last updated on 21/Oct/22

$$\:\:\:\:\:\:\:\:\mathrm{He}'\mathrm{s}\:\mathrm{one}\:\mathrm{of}\:\mathrm{my}\:\mathrm{favorite}\:\mathrm{teachers}\:\mathrm{and}\:\mathrm{so}\:\mathrm{I}\:\mathrm{recognize}\:\mathrm{his}\:\mathrm{writings},\:\mathrm{his}\:\mathrm{methods}, \\ $$$$\:\mathrm{expressions},\:\mathrm{and}\:\mathrm{type}\:\mathrm{of}\:\mathrm{answers}\:\mathrm{like}\:\mathrm{finding}\:\mathrm{the}\:\mathrm{general}\:\mathrm{term}\:\mathrm{of}\:\mathrm{a}\:\mathrm{progression}, \\ $$$$\:\mathrm{haha}.\:\mathrm{For}\:\mathrm{example}\:\mathrm{Q178467}\:\:\:\mathrm{Q177400}. \\ $$$$\:\mathrm{He}\:\mathrm{loves}\:\mathrm{letting}\:{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{using}\:\mathrm{sinh}\:\mathrm{in}\:\mathrm{calculus}.\:\mathrm{He}\:\mathrm{often}\:\mathrm{uses} \\ $$$$\vee\:\mathrm{and}\:\wedge\:\mathrm{to}\:\mathrm{denote}\:“\mathrm{or}''\:\mathrm{and}\:“\mathrm{and}''.\:\mathrm{He}\:\mathrm{likes}\:\mathrm{saying}\:“\mathrm{I}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate}''\:\mathrm{then} \\ $$$$\mathrm{hits}\:\mathrm{it}\:\mathrm{hard}\:\mathrm{with}\:\mathrm{a}\:\mathrm{tough}\:\mathrm{solution}.\:\mathrm{He}\:\mathrm{also}\:\mathrm{says}\:“\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy}''\:\mathrm{when}\:\mathrm{he}'\mathrm{s}\:\mathrm{busy}\:\mathrm{to} \\ $$$$\mathrm{continue},\:“\mathrm{I}\:\mathrm{get}''.\:\mathrm{And}\:\mathrm{lastly}\:\mathrm{we}'\mathrm{re}\:\mathrm{very}\:\mathrm{few}\:\mathrm{in}\:\mathrm{this}\:\mathrm{forum}\:\mathrm{who}\:\mathrm{use}\:\mathrm{Ostrogradsky} \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{was}\:\mathrm{he}\:\mathrm{who}\:\mathrm{introduced}\:\mathrm{it}\:\mathrm{here}\:\mathrm{as}\:\mathrm{far}\:\mathrm{as}\:\mathrm{I}\:\mathrm{know}\left(\mathrm{I}\:\mathrm{learnt}\:\mathrm{it}\:\mathrm{too}\:\mathrm{from}\:\mathrm{him}\right).\: \\ $$$$\mathrm{It}\:\mathrm{wasn}'\mathrm{t}\:\mathrm{difficult}.\:\mathrm{Haha}\:!\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{intend}\:\mathrm{to}\:\mathrm{call}\:\mathrm{him}\:\mathrm{MJS}\:\mathrm{here}.\:\mathrm{Just}\:\mathrm{that}\:\mathrm{he}\:\mathrm{ignored}\:\:\:\: \\ $$$$\mathrm{my}\:\mathrm{greetings}. \\ $$😂😄😅
Commented by ARUNG_Brandon_MBU last updated on 21/Oct/22
Q177400
Commented by Rasheed.Sindhi last updated on 21/Oct/22
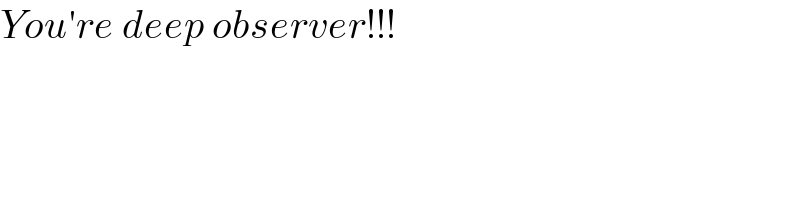
$${You}'{re}\:{deep}\:{observer}!!! \\ $$
Commented by ARUNG_Brandon_MBU last updated on 21/Oct/22
����
Commented by MJS_new last updated on 22/Oct/22

$$\mathrm{Mr}.\:\mathrm{Sherlock}\:\mathrm{Holmes}\:\mathrm{please}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{I}\:\mathrm{should} \\ $$$$\mathrm{have}\:\mathrm{2}\:\mathrm{accounts}?\:{Her}\:{Majesty}\:\mathrm{had}\:\mathrm{been}\:\mathrm{my} \\ $$$$\mathrm{personal}\:\mathrm{defense}\:\mathrm{against}\:\mathrm{the}\:\mathrm{weirdness}\:\mathrm{which} \\ $$$$\mathrm{had}\:\mathrm{been}\:\mathrm{creeping}\:\mathrm{into}\:\mathrm{this}\:\mathrm{forum}\:\mathrm{in}\:\mathrm{those}\:\mathrm{days}… \\ $$$$\mathrm{but}\:\mathrm{now}?\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{my}\:\mathrm{fault}\:\mathrm{when}\:\mathrm{someone}\:\mathrm{uses} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{language}\:\mathrm{as}\:\mathrm{me}. \\ $$
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
�� oh! "Her Majesty had been my personal defense against the weirdness which had been creeping into this forum in those days"
But back then:-
Her Majesty: "I have told you several times I am not MJS believe it or not."
���� You're funny, Sir. You made my day ��
Commented by Rasheed.Sindhi last updated on 22/Oct/22

$${f}\left({person}\right)={account} \\ $$$${Certainly}\:{f}\:{is}\:{NOT}\:{afunction}. \\ $$$${So}\:{f}\left(\boldsymbol{\mathrm{Person}}\right)=\mathrm{MJS},\mathrm{Frix},…{is}\: \\ $$$${possible}.{I}'{m}\:{talking}\:{only}\:{about} \\ $$$$\boldsymbol{{possibility}}.{What}\:{is}\:{the}\:{probability} \\ $$$${that}\:\mathrm{MJS}=\mathrm{Frix}\:?\:\mathcal{T}{his}\:{is}\:{an}\:{interesting} \\ $$$${question}\:{of}\:{probablity}\:{for}\:{forum} \\ $$$${members}.{I}'{m}\:{weak}\:{in}\:{this} \\ $$$${area}\:{but}\:{I}\:{think}\:{Mr}\:{Ar}\:{Brandon}'{s} \\ $$$${probability}\:{of}\:{correctness}\:{will}\:{be} \\ $$$${more}\:{than}\:{any}\:{other}\:{person}\:\left({except}\right. \\ $$$$\left.{M}\left.{JS}/{Frix}\right)\:{in}\:{this}\:{connection}\::\right) \\ $$
Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22
���� Nice week-end to you, Sir RS ! Thanks for your company.
Commented by Rasheed.Sindhi last updated on 22/Oct/22
��������
Commented by peter frank last updated on 22/Oct/22

$$\mathrm{great}\:\mathrm{sir}\:\mathrm{Frix} \\ $$
Commented by Frix last updated on 24/Oct/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
