Question Number 44704 by Tawa1 last updated on 03/Oct/18

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\::\:\:\:\:\:\:\:\:\:\:\:\mathrm{311x}\:−\:\mathrm{112y}\:=\:\mathrm{73} \\ $$
Answered by Joel578 last updated on 04/Oct/18
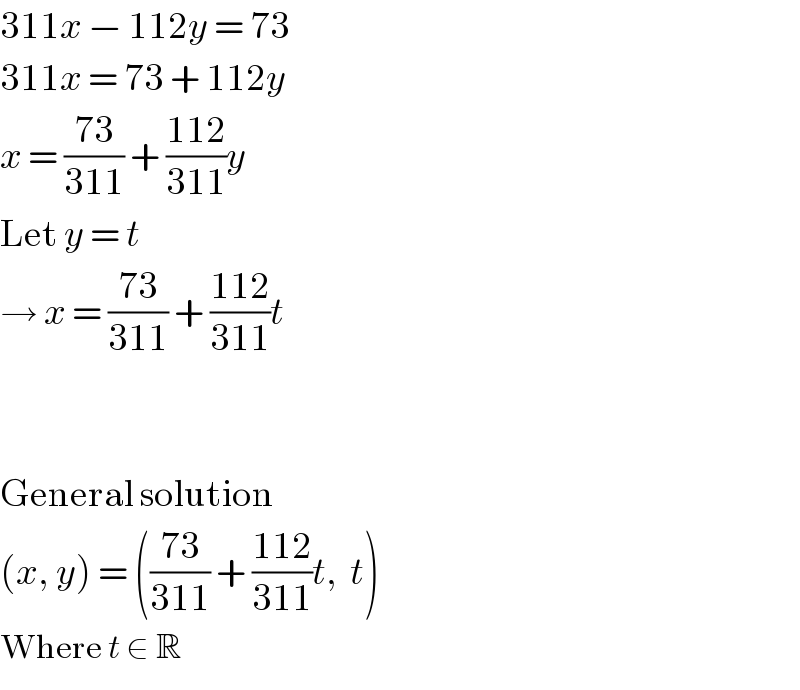
$$\mathrm{311}{x}\:−\:\mathrm{112}{y}\:=\:\mathrm{73} \\ $$$$\mathrm{311}{x}\:=\:\mathrm{73}\:+\:\mathrm{112}{y} \\ $$$${x}\:=\:\frac{\mathrm{73}}{\mathrm{311}}\:+\:\frac{\mathrm{112}}{\mathrm{311}}{y} \\ $$$$\mathrm{Let}\:{y}\:=\:{t} \\ $$$$\rightarrow\:{x}\:=\:\frac{\mathrm{73}}{\mathrm{311}}\:+\:\frac{\mathrm{112}}{\mathrm{311}}{t} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{General}\:\mathrm{solution} \\ $$$$\left({x},\:{y}\right)\:=\:\left(\frac{\mathrm{73}}{\mathrm{311}}\:+\:\frac{\mathrm{112}}{\mathrm{311}}{t},\:\:{t}\right) \\ $$$$\mathrm{Where}\:{t}\:\in\:\mathbb{R} \\ $$
Commented by Tawa1 last updated on 03/Oct/18

$$\mathrm{How}\:\mathrm{sir} \\ $$
Commented by MrW3 last updated on 04/Oct/18

$${I}\:{think}\:{you}\:{mean}\:{a}\:{general}\:\:{integer} \\ $$$${solution}.\:{It}\:{is}\:{then} \\ $$$${x}=\mathrm{15}+\mathrm{112}{n} \\ $$$${y}=\mathrm{41}+\mathrm{311}{n} \\ $$$${with}\:{n}={any}\:{integer} \\ $$$$ \\ $$$${please}\:{have}\:{a}\:{look}\:{at}\:{Q}\mathrm{19198}. \\ $$
Commented by Tawa1 last updated on 04/Oct/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{go}\:\mathrm{through}\:\mathrm{your}\:\mathrm{explanation}\:\mathrm{and}\:\mathrm{get}\:\mathrm{back}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 04/Oct/18

$$\mathrm{Please}\:\mathrm{sir}.\:\mathrm{brush}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{study}\:\mathrm{it}\:\mathrm{sir} \\ $$
Answered by MrW3 last updated on 05/Oct/18

$${How}\:{to}\:{find}\:{the}\:{general}\:{solution}\:{of} \\ $$$$\mathrm{311}{x}−\mathrm{112}{y}=\mathrm{73}\:{with}\:{x},{y}\in\mathbb{Z} \\ $$$$ \\ $$$${Step}\:\mathrm{1}:\:{find}\:{the}\:{gcd}\:{of}\:\mathrm{311}\:{and}\:\mathrm{112}. \\ $$$$\mathrm{311}=\mathrm{2}×\mathrm{112}+\mathrm{87} \\ $$$$\mathrm{112}=\mathrm{1}×\mathrm{87}+\mathrm{25} \\ $$$$\mathrm{87}=\mathrm{3}×\mathrm{25}+\mathrm{12} \\ $$$$\mathrm{25}=\mathrm{2}×\mathrm{12}+\mathrm{1}\:\leftarrow\:{gcd}\:{from}\:\mathrm{311}\:{an}\:\mathrm{112} \\ $$$$\mathrm{12}=\mathrm{12}×\mathrm{1}+\mathrm{0} \\ $$$$\Rightarrow{gcd}\left(\mathrm{311},\mathrm{112}\right)=\mathrm{1}\:{and}\:{this}\:{divides}\:\mathrm{73} \\ $$$$\Rightarrow{infinite}\:{solutions}\:{exist}. \\ $$$$ \\ $$$${Step}\:\mathrm{2}:\:{find}\:{a}\:{particular}\:{solution}. \\ $$$$\mathrm{73}=\mathrm{3}×\mathrm{25}−\mathrm{2}×\mathrm{1} \\ $$$$=\mathrm{3}×\mathrm{25}−\mathrm{2}×\left(\mathrm{25}−\mathrm{2}×\mathrm{12}\right) \\ $$$$=\mathrm{25}+\mathrm{4}×\mathrm{12} \\ $$$$=\mathrm{25}+\mathrm{4}×\left(\mathrm{87}−\mathrm{3}×\mathrm{25}\right) \\ $$$$=\mathrm{4}×\mathrm{87}−\mathrm{11}×\mathrm{25} \\ $$$$=\mathrm{4}×\mathrm{87}−\mathrm{11}×\left(\mathrm{112}−\mathrm{1}×\mathrm{87}\right) \\ $$$$=\mathrm{15}×\mathrm{87}−\mathrm{11}×\mathrm{112} \\ $$$$=\mathrm{15}×\left(\mathrm{311}−\mathrm{2}×\mathrm{112}\right)−\mathrm{11}×\mathrm{112} \\ $$$$=\mathrm{15}×\mathrm{311}−\mathrm{41}×\mathrm{112} \\ $$$${i}.{e}.\:{x}=\mathrm{15}\:{and}\:{y}=\mathrm{41}\:{is}\:{a}\:{solution}, \\ $$$${since}\:\mathrm{311}×\mathrm{15}−\mathrm{112}×\mathrm{41}=\mathrm{73} \\ $$$$ \\ $$$${Step}\:\mathrm{3}:\:{find}\:{the}\:{general}\:{solution}. \\ $$$${x}=\mathrm{15}+\mathrm{112}{n} \\ $$$${y}=\mathrm{41}+\mathrm{311}{n}\:{with}\:{n}\in\mathbb{Z} \\ $$$$ \\ $$$${This}\:{can}\:{be}\:{easily}\:{checked}: \\ $$$$\mathrm{311}×\left(\mathrm{15}+\mathrm{112}{n}\right)−\mathrm{112}×\left(\mathrm{41}+\mathrm{311}{n}\right) \\ $$$$=\left(\mathrm{311}×\mathrm{15}−\mathrm{112}×\mathrm{41}\right)+\left(\mathrm{311}×\mathrm{112}{n}−\mathrm{112}×\mathrm{311}{n}\right) \\ $$$$=\mathrm{73}+\mathrm{0} \\ $$$$=\mathrm{73} \\ $$
Commented by Tawa1 last updated on 04/Oct/18
$$\mathrm{Yes}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:\mathrm{sir} \\ $$
