Question Number 58785 by naka3546 last updated on 30/Apr/19

$${Find}\:\:{the}\:\:{general}\:\:{solution}\:\:{of}\:\:\:{differential}\:\:{equation}\:\:{below}\:\:: \\ $$$$\left(\mathrm{cos}\:{x}\:\mathrm{cos}\:{y}\:+\:\mathrm{sin}^{\mathrm{2}} {x}\right)\:{dx}\:\:−\:\left(\mathrm{sin}\:{x}\:\mathrm{sin}\:{y}\:+\:\mathrm{cos}^{\mathrm{2}} {y}\right)\:{dy}\:\:=\:\:\mathrm{0} \\ $$
Answered by tanmay last updated on 30/Apr/19
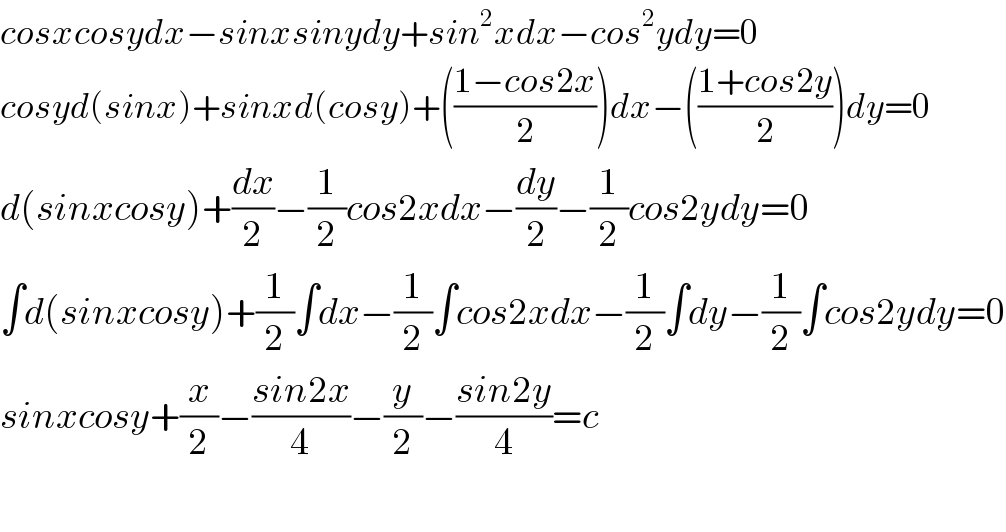
$${cosxcosydx}−{sinxsinydy}+{sin}^{\mathrm{2}} {xdx}−{cos}^{\mathrm{2}} {ydy}=\mathrm{0} \\ $$$${cosyd}\left({sinx}\right)+{sinxd}\left({cosy}\right)+\left(\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}\right){dx}−\left(\frac{\mathrm{1}+{cos}\mathrm{2}{y}}{\mathrm{2}}\right){dy}=\mathrm{0} \\ $$$${d}\left({sinxcosy}\right)+\frac{{dx}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{xdx}−\frac{{dy}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{ydy}=\mathrm{0} \\ $$$$\int{d}\left({sinxcosy}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\mathrm{2}{xdx}−\frac{\mathrm{1}}{\mathrm{2}}\int{dy}−\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\mathrm{2}{ydy}=\mathrm{0} \\ $$$${sinxcosy}+\frac{{x}}{\mathrm{2}}−\frac{{sin}\mathrm{2}{x}}{\mathrm{4}}−\frac{{y}}{\mathrm{2}}−\frac{{sin}\mathrm{2}{y}}{\mathrm{4}}={c} \\ $$$$ \\ $$
