Menu Close

Find-the-general-solution-of-the-equation-3-sin-2x-2-cos-2-x-3-1-sin-2x-2-sin-2-x-28-

Tinku Tara 0 Comments
Pin




Question Number 14632 by Tinkutara last updated on 03/Jun/17
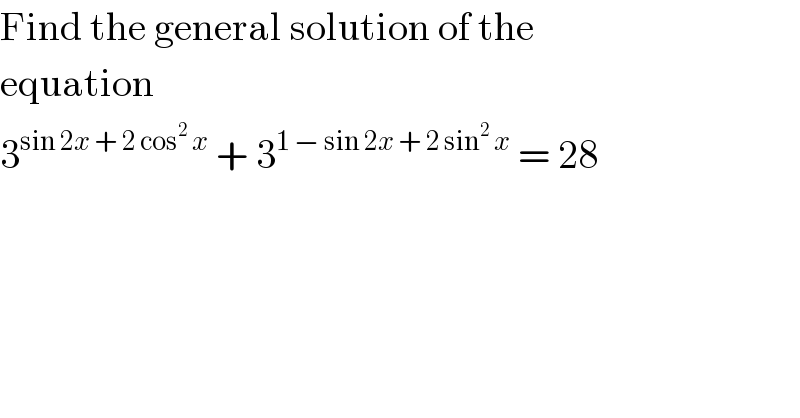
Find the general solution of the equation 3^(sin 2x + 2 cos^2 x) + 3^(1 − sin 2x + 2 sin^2 x) = 28
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation} \\ $$$$\mathrm{3}^{\mathrm{sin}\:\mathrm{2}{x}\:+\:\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:{x}} \:+\:\mathrm{3}^{\mathrm{1}\:−\:\mathrm{sin}\:\mathrm{2}{x}\:+\:\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}} \:=\:\mathrm{28} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 03/Jun/17
sin2x+2cos^2 x=m⇒1−sin2x+2sin^2 x= =1−sin2x+2−2cos^2 x=3−m ⇒3^m +3^(3−m) =28⇒(3^m =t) t^2 −28t+27=0⇒t=1,27 1)3^m =1⇒sin2x+2cos^2 x−1=0⇒ sin2x+cos2x=0⇒tg2x=0⇒x=((kπ)/2) (cos2x≠0⇒2x≠2lπ+(π/2)⇒x≠lπ+(π/4)) 2)3^m =27=3^3 ⇒m=3 ⇒sin2x+2cos^2 x=3⇒sin2x+cos2x=2 ⇒(√2)sin(2x+(π/4))=2⇒sin(2x+(π/4))=(√2) it is impossible.^
$${sin}\mathrm{2}{x}+\mathrm{2}{cos}^{\mathrm{2}} {x}={m}\Rightarrow\mathrm{1}−{sin}\mathrm{2}{x}+\mathrm{2}{sin}^{\mathrm{2}} {x}= \\ $$$$=\mathrm{1}−{sin}\mathrm{2}{x}+\mathrm{2}−\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{3}−{m} \\ $$$$\Rightarrow\mathrm{3}^{{m}} +\mathrm{3}^{\mathrm{3}−{m}} =\mathrm{28}\Rightarrow\left(\mathrm{3}^{{m}} ={t}\right) \\ $$$${t}^{\mathrm{2}} −\mathrm{28}{t}+\mathrm{27}=\mathrm{0}\Rightarrow{t}=\mathrm{1},\mathrm{27} \\ $$$$\left.\mathrm{1}\right)\mathrm{3}^{{m}} =\mathrm{1}\Rightarrow{sin}\mathrm{2}{x}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}=\mathrm{0}\Rightarrow \\ $$$${sin}\mathrm{2}{x}+{cos}\mathrm{2}{x}=\mathrm{0}\Rightarrow{tg}\mathrm{2}{x}=\mathrm{0}\Rightarrow{x}=\frac{{k}\pi}{\mathrm{2}} \\ $$$$\left({cos}\mathrm{2}{x}\neq\mathrm{0}\Rightarrow\mathrm{2}{x}\neq\mathrm{2}{l}\pi+\frac{\pi}{\mathrm{2}}\Rightarrow{x}\neq{l}\pi+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{3}^{{m}} =\mathrm{27}=\mathrm{3}^{\mathrm{3}} \Rightarrow{m}=\mathrm{3} \\ $$$$\Rightarrow{sin}\mathrm{2}{x}+\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{3}\Rightarrow{sin}\mathrm{2}{x}+{cos}\mathrm{2}{x}=\mathrm{2} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}\Rightarrow{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}} \\ $$$${it}\:{is}\:{impossible}\overset{} {.} \\ $$
Commented by Tinkutara last updated on 04/Jun/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by 433 last updated on 03/Jun/17
3^(sin2x+2(1−sin^2 x)) +3^(1−sin2x+2sin^2 x) =28 3^(sin2x−2sin^2 x+2) +3^(1−sin2x+2sin^2 x) =28 3^(sin2x−2sin^2 x) =y>0 y×3^2 +(3/y)=28 9y^2 −28y+3=0 Δ=28^2 −4×9×3=676=26^2 y_(1,2) =((28±26)/(18))=(1/9) or 3 3^(sin2x−2sin^2 x) =(1/9) sin2x−2sin^2 x=−2 2sinxcosx−2(1−cos^2 x)=−2 2sinxcosx+2cos^2 x=0 2cosx(sinx+cosx)=0 cosx=0 ⇔ x=2kπ±(π/2) sinx=−cosx ⇔ −(sin−x)=−cosx sin(−x)=sin((π/2)−x) −x=2kπ+(π/2)−x ⇔2kπ+π/2=0 −x=2kπ+x+(π/2) ⇔ x=kπ−(π/4) 3^(sin2x−2sin^2 x) =3 sin2x−2sin^2 x=1 2sinxcosx−2(1−cos^2 x)=1 2cosx(sinx+cosx)=3 sin(2x+(π/4))=((√2)/2)(sin2x+cos2x)= ((√2)/2)(2sinxcosx+cos^2 x−sin^2 x) sin(2x+(π/4))×(√2)+1=2sinxcosx+cos^2 x−sin^2 x+1= 2sinxcosx+2cos^2 x=2cosx(sinx+cosx) ⇒ sin(2x+(π/4))×(√2)+1=3 sin(2x+(π/4))=(√2)
$$ \\ $$$$ \\ $$$$\mathrm{3}^{{sin}\mathrm{2}{x}+\mathrm{2}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)} +\mathrm{3}^{\mathrm{1}−{sin}\mathrm{2}{x}+\mathrm{2}{sin}^{\mathrm{2}} {x}} =\mathrm{28} \\ $$$$\mathrm{3}^{{sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{2}} +\mathrm{3}^{\mathrm{1}−{sin}\mathrm{2}{x}+\mathrm{2}{sin}^{\mathrm{2}} {x}} =\mathrm{28} \\ $$$$\mathrm{3}^{{sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}} ={y}>\mathrm{0} \\ $$$${y}×\mathrm{3}^{\mathrm{2}} +\frac{\mathrm{3}}{{y}}=\mathrm{28} \\ $$$$\mathrm{9}{y}^{\mathrm{2}} −\mathrm{28}{y}+\mathrm{3}=\mathrm{0} \\ $$$$\Delta=\mathrm{28}^{\mathrm{2}} −\mathrm{4}×\mathrm{9}×\mathrm{3}=\mathrm{676}=\mathrm{26}^{\mathrm{2}} \\ $$$${y}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{28}\pm\mathrm{26}}{\mathrm{18}}=\frac{\mathrm{1}}{\mathrm{9}}\:{or}\:\mathrm{3} \\ $$$$\mathrm{3}^{{sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}} =\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}=−\mathrm{2} \\ $$$$\mathrm{2}{sinxcosx}−\mathrm{2}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)=−\mathrm{2} \\ $$$$\mathrm{2}{sinxcosx}+\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{0} \\ $$$$\mathrm{2}{cosx}\left({sinx}+{cosx}\right)=\mathrm{0} \\ $$$${cosx}=\mathrm{0}\:\Leftrightarrow\:{x}=\mathrm{2}{k}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$${sinx}=−{cosx}\:\Leftrightarrow\:−\left({sin}−{x}\right)=−{cosx} \\ $$$${sin}\left(−{x}\right)={sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$−{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}}−{x}\:\Leftrightarrow\mathrm{2}{k}\pi+\pi/\mathrm{2}=\mathrm{0}\: \\ $$$$−{x}=\mathrm{2}{k}\pi+{x}+\frac{\pi}{\mathrm{2}}\:\Leftrightarrow\:{x}={k}\pi−\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{3}^{{sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}} =\mathrm{3} \\ $$$${sin}\mathrm{2}{x}−\mathrm{2}{sin}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$$\mathrm{2}{sinxcosx}−\mathrm{2}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)=\mathrm{1} \\ $$$$\mathrm{2}{cosx}\left({sinx}+{cosx}\right)=\mathrm{3} \\ $$$${sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({sin}\mathrm{2}{x}+{cos}\mathrm{2}{x}\right)= \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{2}{sinxcosx}+{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right) \\ $$$${sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)×\sqrt{\mathrm{2}}+\mathrm{1}=\mathrm{2}{sinxcosx}+{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}+\mathrm{1}= \\ $$$$\mathrm{2}{sinxcosx}+\mathrm{2}{cos}^{\mathrm{2}} {x}=\mathrm{2}{cosx}\left({sinx}+{cosx}\right) \\ $$$$\Rightarrow\:{sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)×\sqrt{\mathrm{2}}+\mathrm{1}=\mathrm{3} \\ $$$${sin}\left(\mathrm{2}{x}+\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *