Menu Close

Find-the-greatest-common-divisor-of-1122-and-1001-and-express-the-greatest-common-divisor-d-in-the-form-d-1122x-1001y-Using-the-above-result-solve-the-congruence-equation-37x-11-mod-33-

Tinku Tara 0 Comments
Pin




Question Number 107594 by Rio Michael last updated on 11/Aug/20
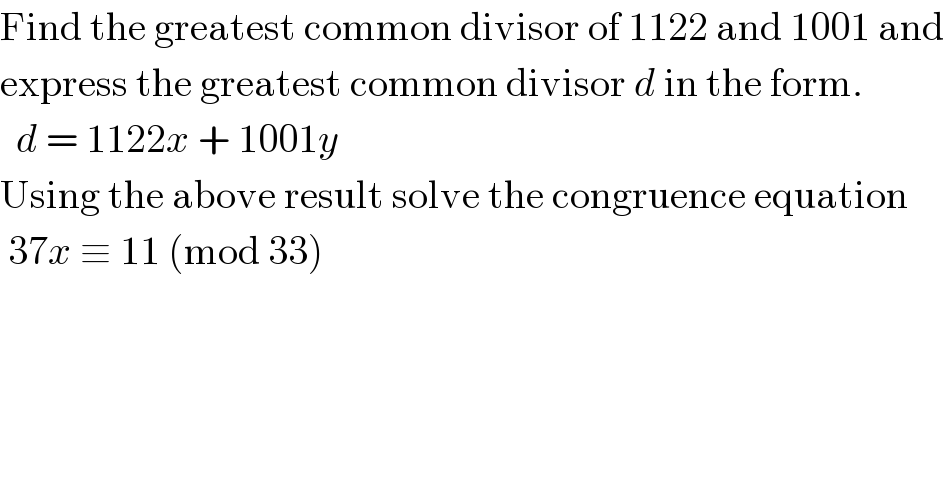
Find the greatest common divisor of 1122 and 1001 and express the greatest common divisor d in the form. d = 1122x + 1001y Using the above result solve the congruence equation 37x ≡ 11 (mod 33)
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{common}\:\mathrm{divisor}\:\mathrm{of}\:\mathrm{1122}\:\mathrm{and}\:\mathrm{1001}\:\mathrm{and}\: \\ $$$$\mathrm{express}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{common}\:\mathrm{divisor}\:{d}\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}. \\ $$$$\:\:{d}\:=\:\mathrm{1122}{x}\:+\:\mathrm{1001}{y} \\ $$$$\mathrm{Using}\:\mathrm{the}\:\mathrm{above}\:\mathrm{result}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{congruence}\:\mathrm{equation} \\ $$$$\:\mathrm{37}{x}\:\equiv\:\mathrm{11}\:\left(\mathrm{mod}\:\mathrm{33}\right) \\ $$
Answered by 1549442205PVT last updated on 11/Aug/20
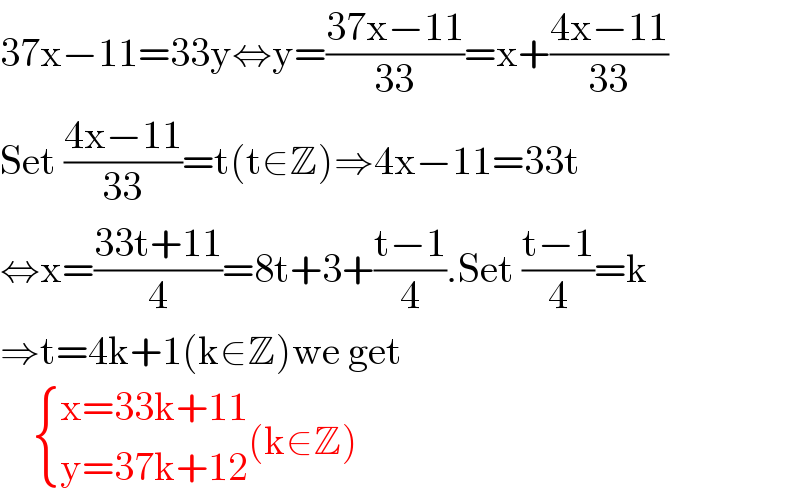
37x−11=33y⇔y=((37x−11)/(33))=x+((4x−11)/(33)) Set ((4x−11)/(33))=t(t∈Z)⇒4x−11=33t ⇔x=((33t+11)/4)=8t+3+((t−1)/4).Set ((t−1)/4)=k ⇒t=4k+1(k∈Z)we get { ((x=33k+11)),((y=37k+12)) :}(k∈Z)
$$\mathrm{37x}−\mathrm{11}=\mathrm{33y}\Leftrightarrow\mathrm{y}=\frac{\mathrm{37x}−\mathrm{11}}{\mathrm{33}}=\mathrm{x}+\frac{\mathrm{4x}−\mathrm{11}}{\mathrm{33}} \\ $$$$\mathrm{Set}\:\frac{\mathrm{4x}−\mathrm{11}}{\mathrm{33}}=\mathrm{t}\left(\mathrm{t}\in\mathbb{Z}\right)\Rightarrow\mathrm{4x}−\mathrm{11}=\mathrm{33t} \\ $$$$\Leftrightarrow\mathrm{x}=\frac{\mathrm{33t}+\mathrm{11}}{\mathrm{4}}=\mathrm{8t}+\mathrm{3}+\frac{\mathrm{t}−\mathrm{1}}{\mathrm{4}}.\mathrm{Set}\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{4}}=\mathrm{k} \\ $$$$\Rightarrow\mathrm{t}=\mathrm{4k}+\mathrm{1}\left(\mathrm{k}\in\mathbb{Z}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\:\:\:\:\begin{cases}{\mathrm{x}=\mathrm{33k}+\mathrm{11}}\\{\mathrm{y}=\mathrm{37k}+\mathrm{12}}\end{cases}\left(\mathrm{k}\in\mathbb{Z}\right) \\ $$
Answered by Aziztisffola last updated on 11/Aug/20
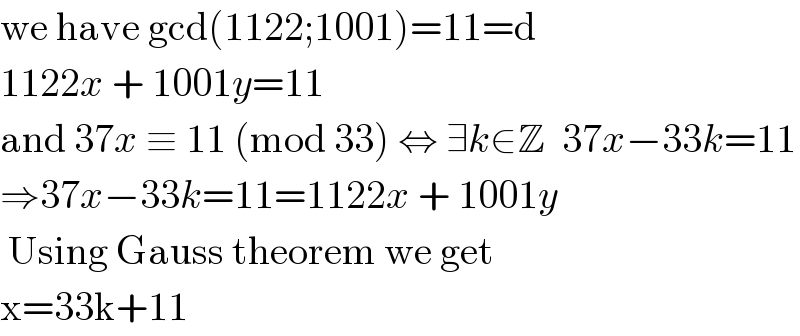
we have gcd(1122;1001)=11=d 1122x + 1001y=11 and 37x ≡ 11 (mod 33) ⇔ ∃k∈Z 37x−33k=11 ⇒37x−33k=11=1122x + 1001y Using Gauss theorem we get x=33k+11
$$\mathrm{we}\:\mathrm{have}\:\mathrm{gcd}\left(\mathrm{1122};\mathrm{1001}\right)=\mathrm{11}=\mathrm{d} \\ $$$$\mathrm{1122}{x}\:+\:\mathrm{1001}{y}=\mathrm{11} \\ $$$$\mathrm{and}\:\mathrm{37}{x}\:\equiv\:\mathrm{11}\:\left(\mathrm{mod}\:\mathrm{33}\right)\:\Leftrightarrow\:\exists{k}\in\mathbb{Z}\:\:\mathrm{37}{x}−\mathrm{33}{k}=\mathrm{11} \\ $$$$\Rightarrow\mathrm{37}{x}−\mathrm{33}{k}=\mathrm{11}=\mathrm{1122}{x}\:+\:\mathrm{1001}{y} \\ $$$$\:\mathrm{Using}\:\mathrm{Gauss}\:\mathrm{theorem}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{x}=\mathrm{33k}+\mathrm{11} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *