Question Number 33406 by NECx last updated on 15/Apr/18
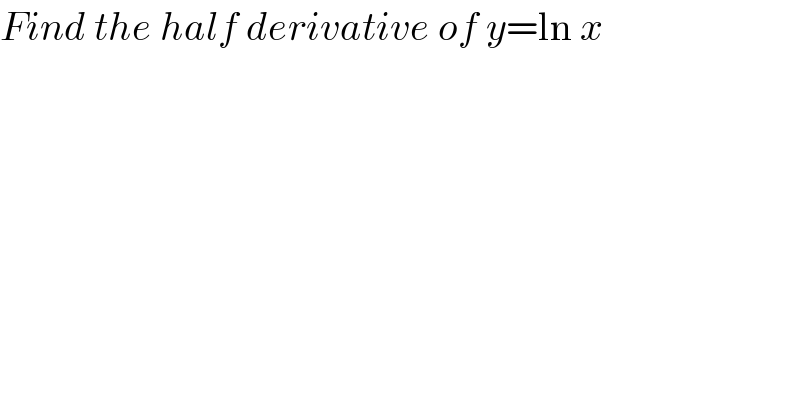
$${Find}\:{the}\:{half}\:{derivative}\:{of}\:{y}=\mathrm{ln}\:{x} \\ $$
Commented by MJS last updated on 15/Apr/18
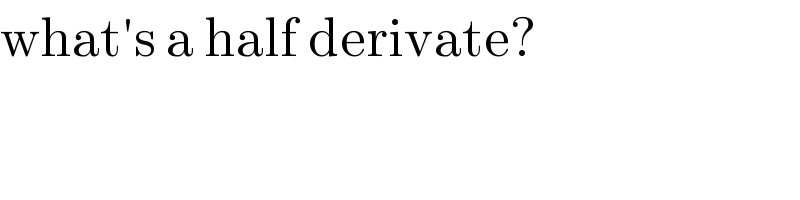
$$\mathrm{what}'\mathrm{s}\:\mathrm{a}\:\mathrm{half}\:\mathrm{derivate}? \\ $$
Commented by NECx last updated on 16/Apr/18

$${I}\:{mean}\:{nth}\:{derivative}\:{rather} \\ $$
Commented by MJS last updated on 16/Apr/18
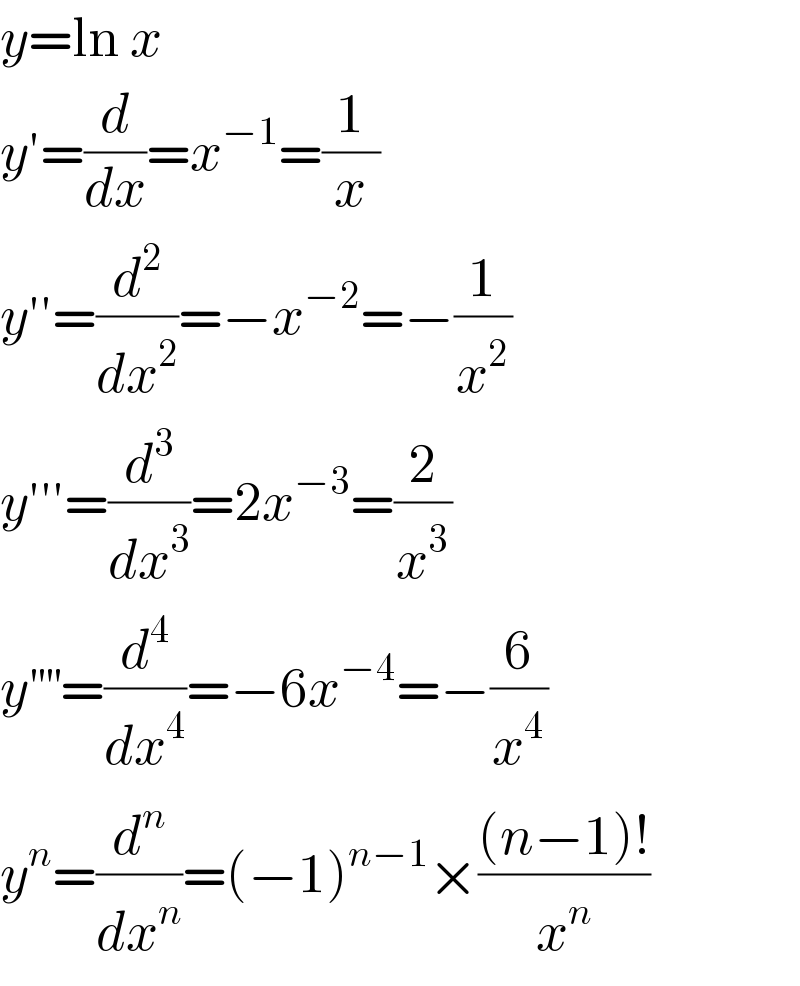
$${y}=\mathrm{ln}\:{x} \\ $$$${y}'=\frac{{d}}{{dx}}={x}^{−\mathrm{1}} =\frac{\mathrm{1}}{{x}} \\ $$$${y}''=\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }=−{x}^{−\mathrm{2}} =−\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${y}'''=\frac{{d}^{\mathrm{3}} }{{dx}^{\mathrm{3}} }=\mathrm{2}{x}^{−\mathrm{3}} =\frac{\mathrm{2}}{{x}^{\mathrm{3}} } \\ $$$${y}^{''''} =\frac{{d}^{\mathrm{4}} }{{dx}^{\mathrm{4}} }=−\mathrm{6}{x}^{−\mathrm{4}} =−\frac{\mathrm{6}}{{x}^{\mathrm{4}} } \\ $$$${y}^{{n}} =\frac{{d}^{{n}} }{{dx}^{{n}} }=\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} ×\frac{\left({n}−\mathrm{1}\right)!}{{x}^{{n}} } \\ $$
Commented by NECx last updated on 16/Apr/18
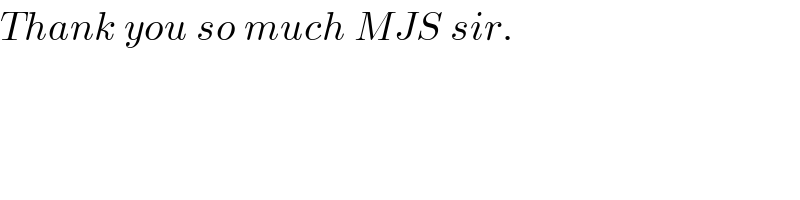
$${Thank}\:{you}\:{so}\:{much}\:{MJS}\:{sir}. \\ $$
