Question Number 104035 by ajfour last updated on 19/Jul/20
$${Find}\:{the}\:{image}\:{of}\:{point}\:\overset{\rightarrow} {{OP}}\:=\:\bar {{p}}\:\:{in} \\ $$$${the}\:{line}\:\:\bar {{r}}=\bar {{a}}+\lambda\bar {{b}}\:. \\ $$
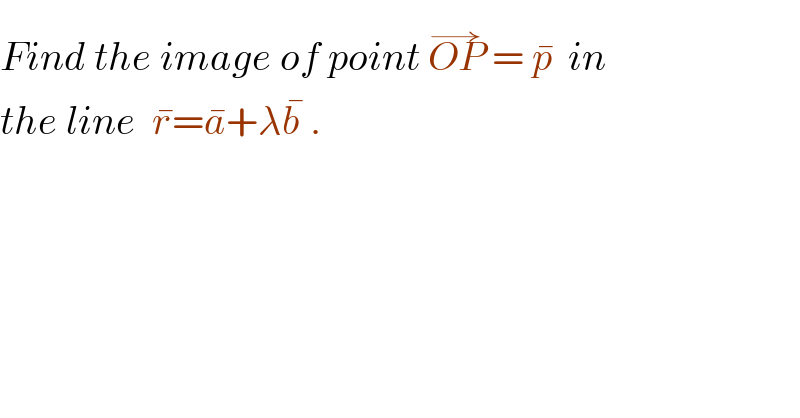
Answered by mr W last updated on 19/Jul/20
Commented by mr W last updated on 19/Jul/20
$${AN}=\lambda{b} \\ $$$$\frac{\left({p}−{a}\right)\centerdot{b}}{\mid{b}\mid}=\lambda\mid{b}\mid \\ $$$$\lambda=\frac{\left({p}−{a}\right)\centerdot{b}}{\mid{b}\mid^{\mathrm{2}} } \\ $$$${PN}={a}+\lambda{b}−{p} \\ $$$${OQ}={q}={p}+\mathrm{2}{PN}={p}+\mathrm{2}\left({a}+\lambda{b}−{p}\right) \\ $$$$=\mathrm{2}\left({a}+\lambda{b}\right)−{p} \\ $$$$\Rightarrow\boldsymbol{{q}}=\mathrm{2}\left(\boldsymbol{{a}}+\frac{\left(\boldsymbol{{p}}−\boldsymbol{{a}}\right)\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{b}}\mid^{\mathrm{2}} }\boldsymbol{{b}}\right)−\boldsymbol{{p}} \\ $$
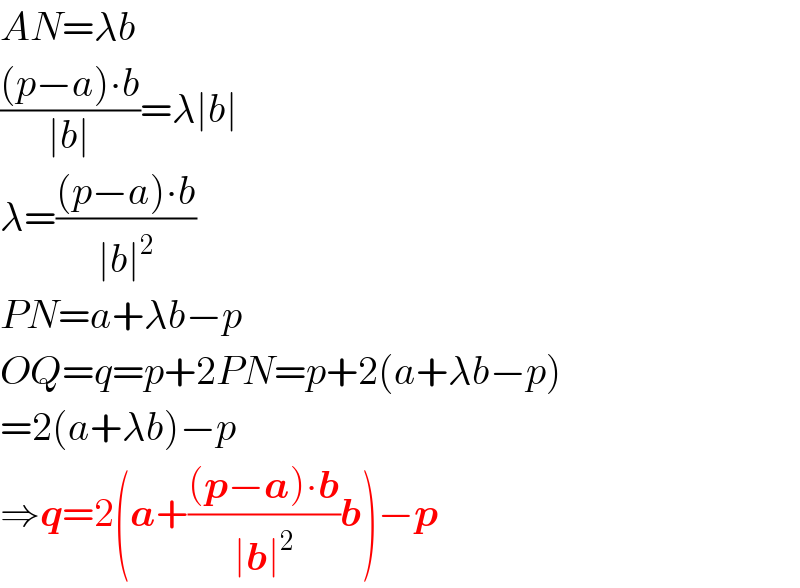
Commented by ajfour last updated on 19/Jul/20
$${I}\:{believe}\:{this}'{ll}\:{be}\:{true}\:{for}\:\mathrm{3}{D}\:{even} \\ $$$${Sir}\:? \\ $$
Commented by mr W last updated on 19/Jul/20
$${basically}\:{yes}. \\ $$
Commented by ajfour last updated on 19/Jul/20
![((p+q)/2)=a+λb ⇒ q=2(a+λb)−p Now (q−p).b=0 [(a+λb)−p].b = 0 λ=(((a−p).b)/(∣b∣^2 )) q^ =(2a^ −p^ )+(((2(a^ −p^ ).b^ )/(∣b^ ∣^2 )))b^](https://www.tinkutara.com/question/Q104075.png)
$$\frac{{p}+{q}}{\mathrm{2}}={a}+\lambda{b}\:\:\:\:\Rightarrow\:\:\:{q}=\mathrm{2}\left({a}+\lambda{b}\right)−{p} \\ $$$${Now}\:\:\:\left({q}−{p}\right).{b}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left[\left({a}+\lambda{b}\right)−{p}\right].{b}\:=\:\mathrm{0} \\ $$$$\lambda=\frac{\left({a}−{p}\right).{b}}{\mid{b}\mid^{\mathrm{2}} } \\ $$$$\bar {{q}}=\left(\mathrm{2}\bar {{a}}−\bar {{p}}\right)+\left(\frac{\mathrm{2}\left(\bar {{a}}−\bar {{p}}\right).\bar {{b}}}{\mid\bar {{b}}\mid^{\mathrm{2}} }\right)\bar {{b}} \\ $$
Commented by mr W last updated on 19/Jul/20
$${yes},\:{thanks}! \\ $$