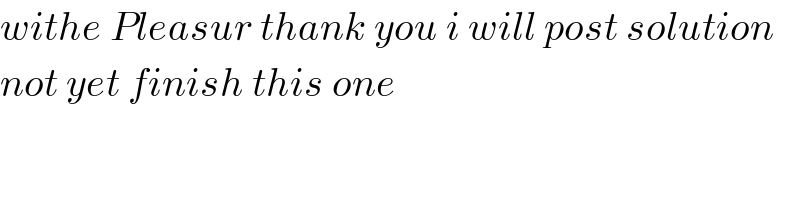Question Number 98929 by Dwaipayan Shikari last updated on 17/Jun/20
![Find[]the[]integral[]of[] ∫(dt/( (√((1+t^(10) )))))](https://www.tinkutara.com/question/Q98929.png)
Commented by maths mind last updated on 17/Jun/20

Commented by M±th+et+s last updated on 17/Jun/20
Commented by maths mind last updated on 18/Jun/20
Commented by M±th+et+s last updated on 18/Jun/20

Commented by M±th+et+s last updated on 18/Jun/20
Commented by maths mind last updated on 20/Jun/20