Question Number 124619 by arkanmath7@gmail.com last updated on 04/Dec/20

$${find}\:{the}\:{inverse}\:{of}\:{y}={x}^{\mathrm{4}} −\mathrm{2}\boldsymbol{{x}}+\mathrm{1} \\ $$
Commented by MJS_new last updated on 04/Dec/20

$${x}^{\mathrm{4}} −\mathrm{2}{x}−\left({y}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=? \\ $$$$\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{the}\:\mathrm{complete}\:\mathrm{path} \\ $$$$\mathrm{of}\:\mathrm{Ferrari}.\:\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{easier}\:\mathrm{path};\:\mathrm{if}\:\mathrm{you}\:\mathrm{have} \\ $$$$\mathrm{a}\:\mathrm{solution},\:\mathrm{please}\:\mathrm{share}\:\mathrm{it} \\ $$
Commented by arkanmath7@gmail.com last updated on 04/Dec/20

$${Actually}\:{I}\:{look}\:{for}\:{the}\:{answer} \\ $$
Answered by ajfour last updated on 04/Dec/20
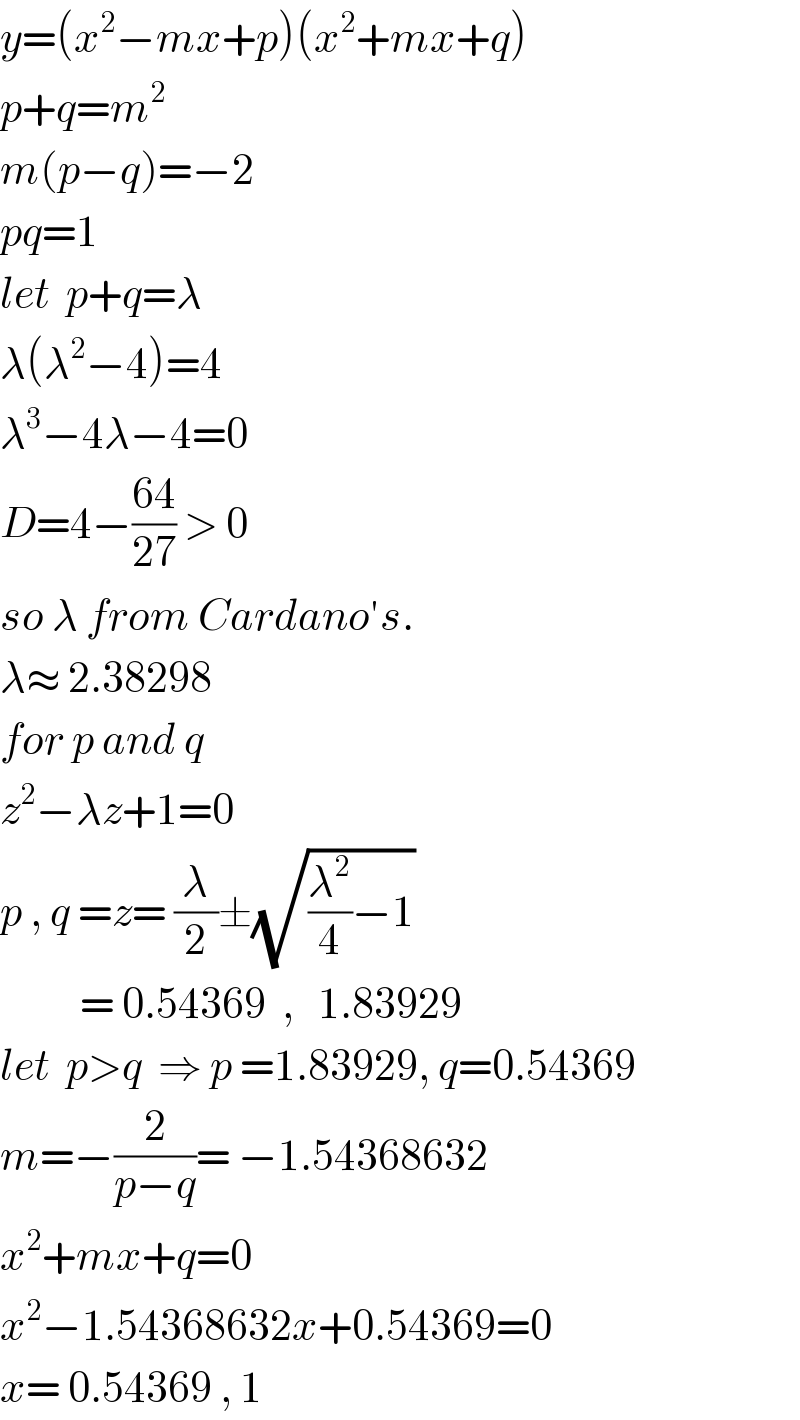
$${y}=\left({x}^{\mathrm{2}} −{mx}+{p}\right)\left({x}^{\mathrm{2}} +{mx}+{q}\right) \\ $$$${p}+{q}={m}^{\mathrm{2}} \\ $$$${m}\left({p}−{q}\right)=−\mathrm{2} \\ $$$${pq}=\mathrm{1} \\ $$$${let}\:\:{p}+{q}=\lambda \\ $$$$\lambda\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{4} \\ $$$$\lambda^{\mathrm{3}} −\mathrm{4}\lambda−\mathrm{4}=\mathrm{0} \\ $$$${D}=\mathrm{4}−\frac{\mathrm{64}}{\mathrm{27}}\:>\:\mathrm{0} \\ $$$${so}\:\lambda\:{from}\:{Cardano}'{s}. \\ $$$$\lambda\approx\:\mathrm{2}.\mathrm{38298} \\ $$$${for}\:{p}\:{and}\:{q} \\ $$$${z}^{\mathrm{2}} −\lambda{z}+\mathrm{1}=\mathrm{0} \\ $$$${p}\:,\:{q}\:={z}=\:\frac{\lambda}{\mathrm{2}}\pm\sqrt{\frac{\lambda^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{0}.\mathrm{54369}\:\:,\:\:\:\mathrm{1}.\mathrm{83929}\: \\ $$$${let}\:\:{p}>{q}\:\:\Rightarrow\:{p}\:=\mathrm{1}.\mathrm{83929},\:{q}=\mathrm{0}.\mathrm{54369} \\ $$$${m}=−\frac{\mathrm{2}}{{p}−{q}}=\:−\mathrm{1}.\mathrm{54368632} \\ $$$${x}^{\mathrm{2}} +{mx}+{q}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{1}.\mathrm{54368632}{x}+\mathrm{0}.\mathrm{54369}=\mathrm{0} \\ $$$${x}=\:\mathrm{0}.\mathrm{54369}\:,\:\mathrm{1} \\ $$
