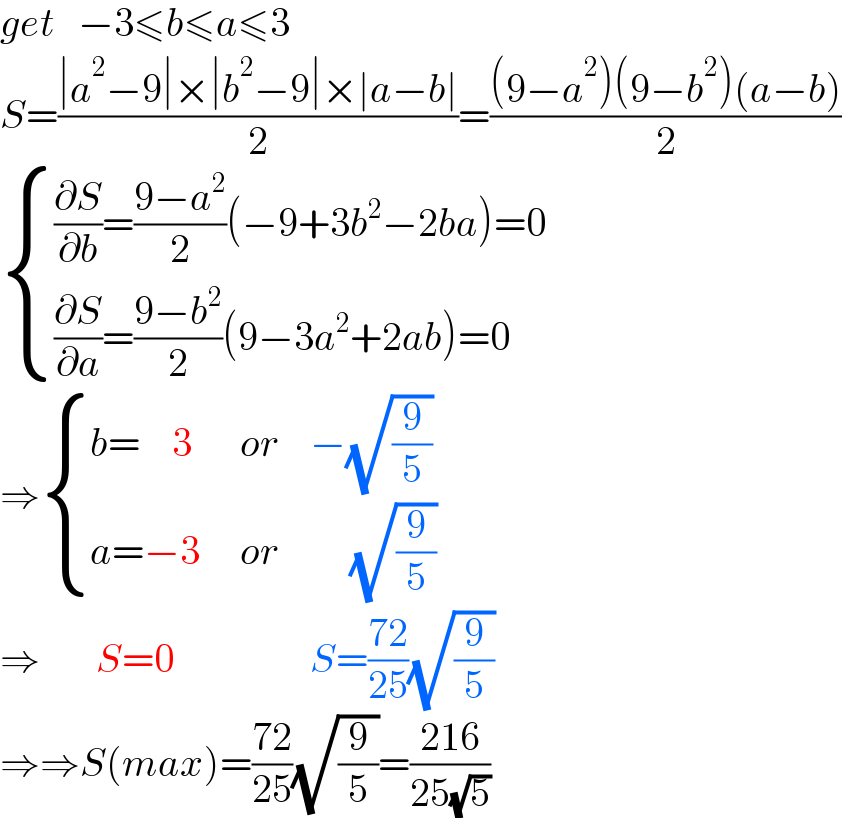Question Number 185453 by cortano1 last updated on 22/Jan/23

Commented by mr W last updated on 22/Jan/23
Commented by cortano1 last updated on 22/Jan/23
Commented by cortano1 last updated on 22/Jan/23
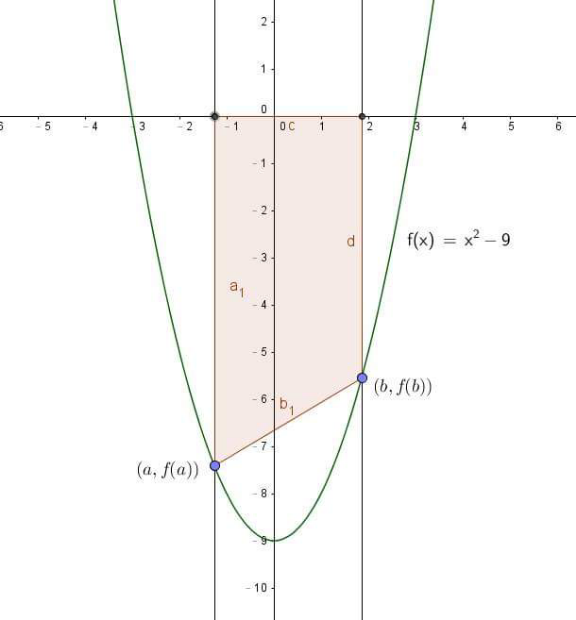
Commented by mathlove last updated on 22/Jan/23
Commented by mr W last updated on 22/Jan/23
Commented by mr W last updated on 22/Jan/23
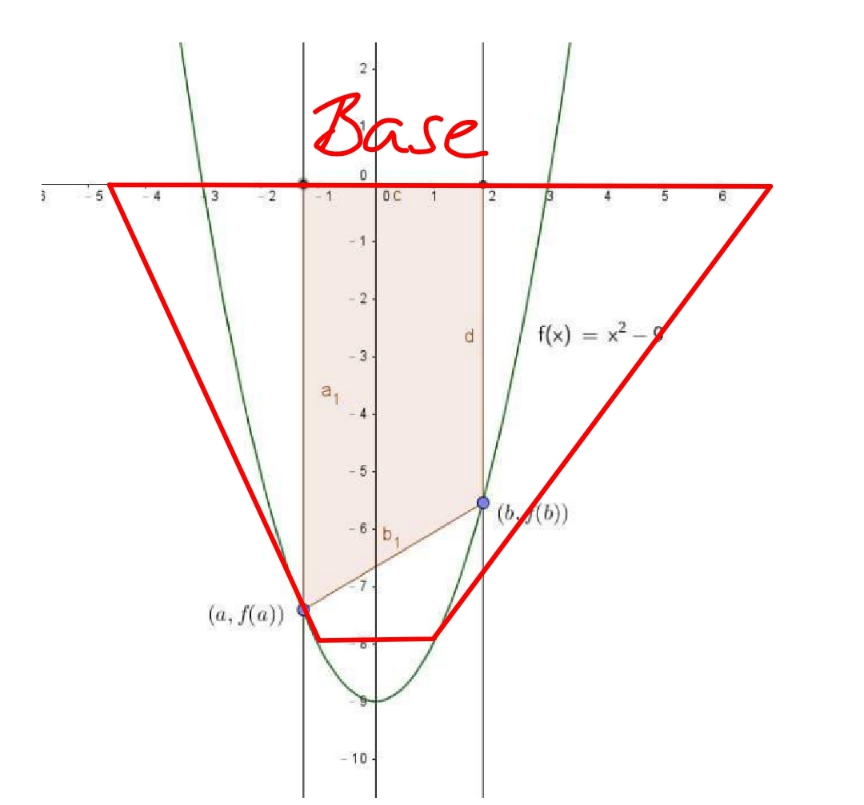
Commented by mr W last updated on 22/Jan/23
Commented by cortano1 last updated on 22/Jan/23

Commented by mr W last updated on 22/Jan/23

Answered by mahdipoor last updated on 22/Jan/23