Question Number 112996 by Aina Samuel Temidayo last updated on 10/Sep/20
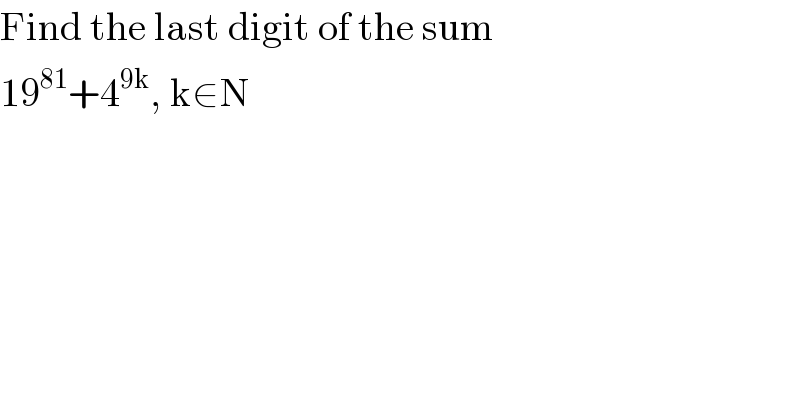
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} ,\:\mathrm{k}\in\mathrm{N} \\ $$
Answered by Aziztisffola last updated on 10/Sep/20
![19^(81) +4^(9k) ≡?[10] 19≡9≡−1[10]⇒19^(81) ≡(−1)^(81) [10]≡−1[10] 4^9 ≡4[10]⇒4^(9k) ≡4^k [10] ⇒19^(81) +4^(9k) ≡4^k −1[10] k=0 ⇒last digit is 0 k=1⇒....is 3 k=2⇒....is 5 k=3⇒....is 3 k=4⇒....is 5 ..... if k=even ⇒last digit of 19^(81) +4^(9k) , k∈N is 5 and if k=odd then last digit of 19^(81) +4^(9k) , k∈N is 3.](https://www.tinkutara.com/question/Q113013.png)
$$\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} \equiv?\left[\mathrm{10}\right] \\ $$$$\mathrm{19}\equiv\mathrm{9}\equiv−\mathrm{1}\left[\mathrm{10}\right]\Rightarrow\mathrm{19}^{\mathrm{81}} \equiv\left(−\mathrm{1}\right)^{\mathrm{81}} \left[\mathrm{10}\right]\equiv−\mathrm{1}\left[\mathrm{10}\right] \\ $$$$\mathrm{4}^{\mathrm{9}} \equiv\mathrm{4}\left[\mathrm{10}\right]\Rightarrow\mathrm{4}^{\mathrm{9k}} \equiv\mathrm{4}^{\mathrm{k}} \left[\mathrm{10}\right] \\ $$$$\Rightarrow\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} \equiv\mathrm{4}^{\mathrm{k}} −\mathrm{1}\left[\mathrm{10}\right] \\ $$$$\mathrm{k}=\mathrm{0}\:\Rightarrow\mathrm{last}\:\mathrm{digit}\:\mathrm{is}\:\mathrm{0} \\ $$$$\mathrm{k}=\mathrm{1}\Rightarrow….\mathrm{is}\:\mathrm{3} \\ $$$$\mathrm{k}=\mathrm{2}\Rightarrow….\mathrm{is}\:\mathrm{5} \\ $$$$\mathrm{k}=\mathrm{3}\Rightarrow….\mathrm{is}\:\mathrm{3} \\ $$$$\mathrm{k}=\mathrm{4}\Rightarrow….\mathrm{is}\:\mathrm{5} \\ $$$$….. \\ $$$$\:\mathrm{if}\:\:\mathrm{k}=\mathrm{even}\:\Rightarrow\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} ,\:\mathrm{k}\in\mathrm{N} \\ $$$$\:\mathrm{is}\:\mathrm{5}\:\mathrm{and}\:\mathrm{if}\:\mathrm{k}=\mathrm{odd}\:\mathrm{then}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{19}^{\mathrm{81}} +\mathrm{4}^{\mathrm{9k}} ,\:\mathrm{k}\in\mathrm{N} \\ $$$$\:\mathrm{is}\:\mathrm{3}. \\ $$
Commented by Aina Samuel Temidayo last updated on 10/Sep/20

$$\mathrm{Yea}. \\ $$
