Question Number 25280 by NECx last updated on 07/Dec/17
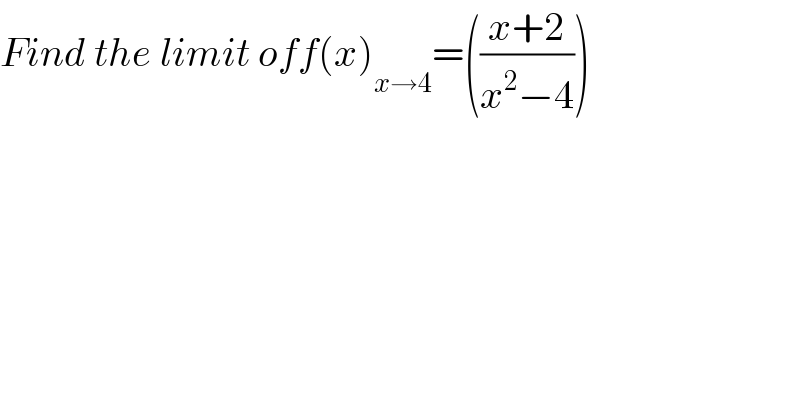
$${Find}\:{the}\:{limit}\:{off}\left({x}\right)\underset{{x}\rightarrow\mathrm{4}} {\:}=\left(\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 07/Dec/17
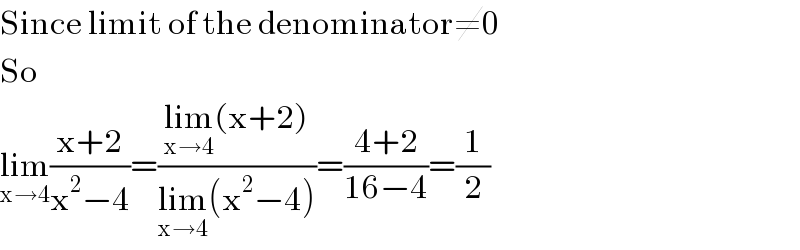
$$\mathrm{Since}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{denominator}\neq\mathrm{0} \\ $$$$\mathrm{So} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}=\frac{\underset{\mathrm{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\mathrm{x}+\mathrm{2}\right)}{\underset{\mathrm{x}\rightarrow\mathrm{4}} {\mathrm{lim}}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)}=\frac{\mathrm{4}+\mathrm{2}}{\mathrm{16}−\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
