Question Number 82494 by niroj last updated on 21/Feb/20
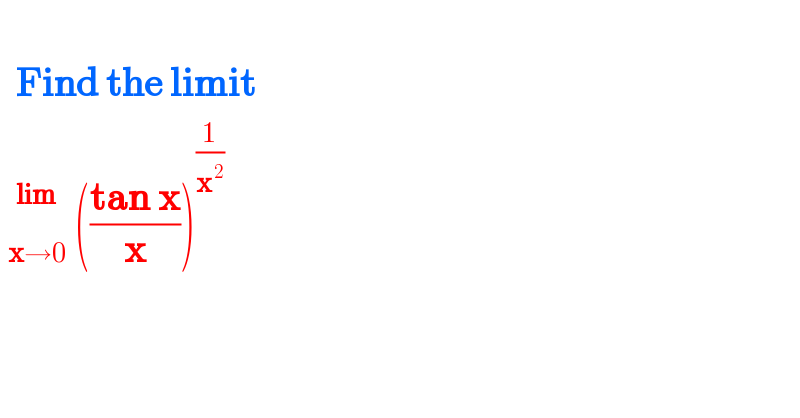
$$\:\: \\ $$$$\:\:\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{limit}} \\ $$$$\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\overset{\boldsymbol{\mathrm{lim}}} {\:}}\:\left(\frac{\boldsymbol{\mathrm{tan}}\:\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}}\right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\:\mathrm{2}} }} \\ $$
Commented by abdomathmax last updated on 21/Feb/20
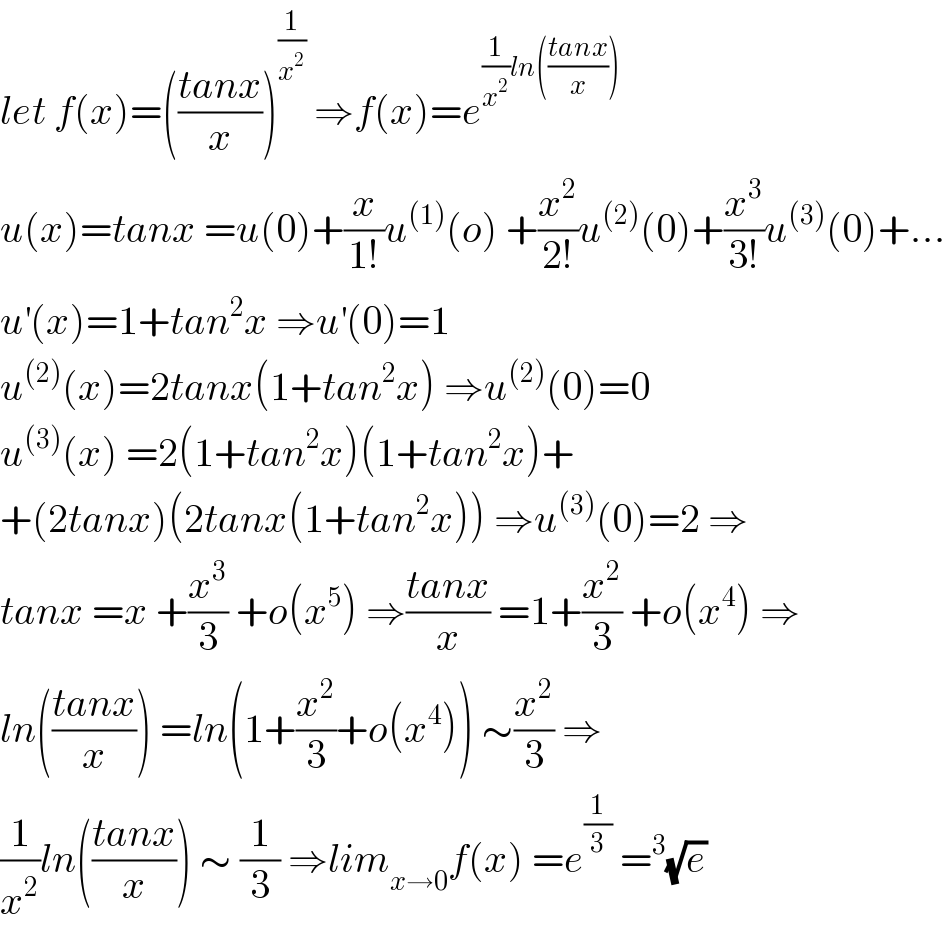
$${let}\:{f}\left({x}\right)=\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:\Rightarrow{f}\left({x}\right)={e}^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{tanx}}{{x}}\right)} \\ $$$${u}\left({x}\right)={tanx}\:={u}\left(\mathrm{0}\right)+\frac{{x}}{\mathrm{1}!}{u}^{\left(\mathrm{1}\right)} \left({o}\right)\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}{u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}{u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)+… \\ $$$${u}^{'} \left({x}\right)=\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\Rightarrow{u}^{'} \left(\mathrm{0}\right)=\mathrm{1} \\ $$$${u}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow{u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$${u}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)+ \\ $$$$+\left(\mathrm{2}{tanx}\right)\left(\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)\:\Rightarrow{u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow \\ $$$${tanx}\:={x}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow\frac{{tanx}}{{x}}\:=\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$${ln}\left(\frac{{tanx}}{{x}}\right)\:={ln}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+{o}\left({x}^{\mathrm{4}} \right)\right)\:\sim\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left(\frac{{tanx}}{{x}}\right)\:\sim\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)\:={e}^{\frac{\mathrm{1}}{\mathrm{3}}} \:=^{\mathrm{3}} \sqrt{{e}} \\ $$
Commented by jagoll last updated on 22/Feb/20
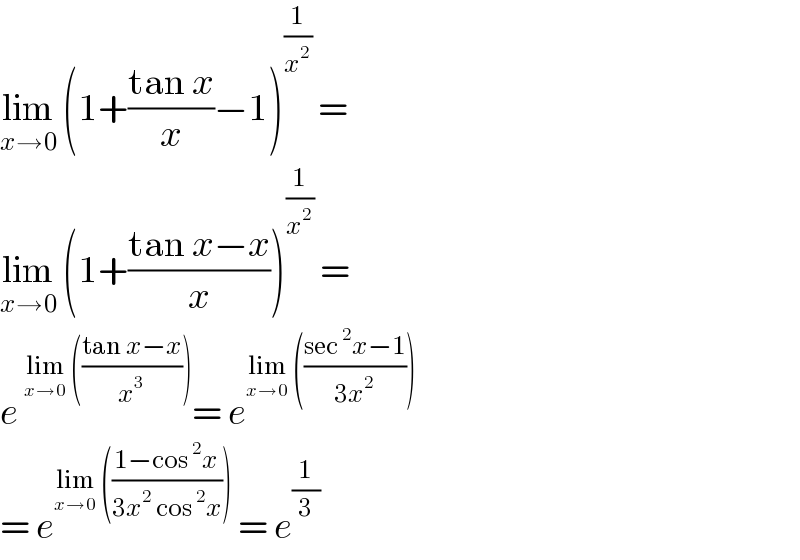
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{tan}\:{x}}{{x}}−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{tan}\:{x}−{x}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:= \\ $$$${e}\:^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:{x}−{x}}{{x}^{\mathrm{3}} }\right)} =\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\right)} \\ $$$$=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{3}{x}^{\mathrm{2}} \:\mathrm{cos}\:^{\mathrm{2}} {x}}\right)} \:=\:{e}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$
Commented by john santu last updated on 22/Feb/20

$${nice} \\ $$
Commented by niroj last updated on 22/Feb/20

$$\:{great}. \\ $$
