find-the-limits-of-1-u-n-k-1-n-n-n-2-k-2-2-v-n-k-1-n-1-n-2-2kn-

Question Number 91667 by Ar Brandon last updated on 02/May/20

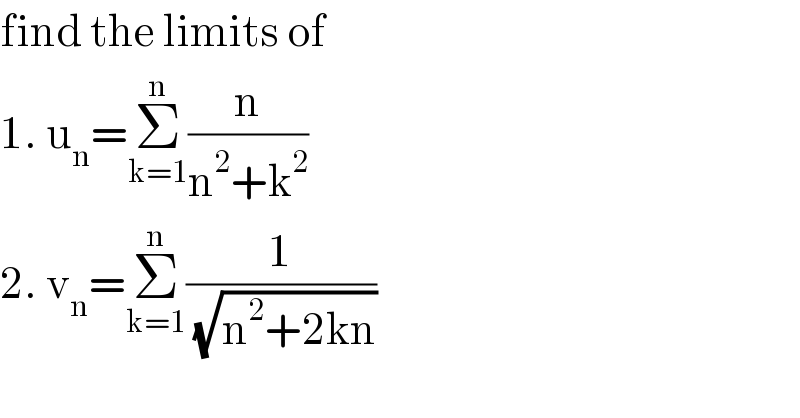
find the limits of 1. u_n =Σ_(k=1) ^n (n/(n^2 +k^2 )) 2. v_n =Σ_(k=1) ^n (1/( (√(n^2 +2kn))))

$$\mathrm{find}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{of}\: \\ $$$$\mathrm{1}.\:\mathrm{u}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} }\:\:\: \\ $$$$\mathrm{2}.\:\mathrm{v}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{2kn}}} \\ $$

Commented by Prithwish Sen 1 last updated on 02/May/20

1.lim_(n→∞) U_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (1/(1+((k/n))^2 )) = ∫_0 ^1 (dx/(1+x^2 )) = tan^(−1) (π/4) 2.lim_(n→∞) V_n = lim_(n→∞) (1/n)Σ_(k=1) ^n (1/( (√(1+2((k/n)))))) = ∫_0 ^1 (dx/( (√(1+2x))))=[(√(1+2x))]_0 ^1 = (√3)−1

$$\mathrm{1}.\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}U}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{2}.\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{V}_{\mathrm{n}} =\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}\left(\frac{\mathrm{k}}{\mathrm{n}}\right)}}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{2x}}}=\left[\sqrt{\mathrm{1}+\mathrm{2x}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\sqrt{\mathrm{3}}−\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 02/May/20

Thanks What′s the relationship between the Σ and ∫ please?

$$\mathrm{Thanks} \\ $$$$\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{relationship}\:\mathrm{between}\:\mathrm{the}\:\Sigma\:\mathrm{and}\:\int \\ $$$$\mathrm{please}? \\ $$

Commented by Ar Brandon last updated on 02/May/20

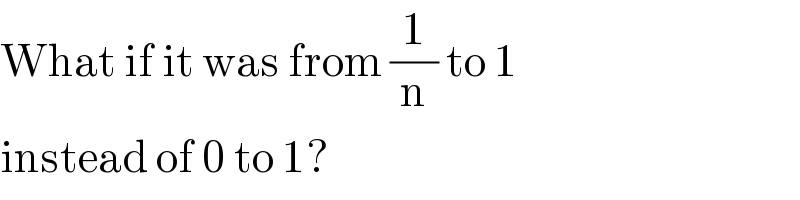
What if it was from (1/n) to 1 instead of 0 to 1?

$$\mathrm{What}\:\mathrm{if}\:\mathrm{it}\:\mathrm{was}\:\mathrm{from}\:\frac{\mathrm{1}}{\mathrm{n}}\:\mathrm{to}\:\mathrm{1}\: \\ $$$$\mathrm{instead}\:\mathrm{of}\:\mathrm{0}\:\mathrm{to}\:\mathrm{1}? \\ $$

Commented by Prithwish Sen 1 last updated on 02/May/20

when you add some discrete entity for a very large number you put Σ like if you add all the natural number from 1 to ∞ you put Σ_(n=1) ^∞ n but if you add an continuos entity such as time which takes all the values in between the natural numbers you use ∫

$$\mathrm{when}\:\mathrm{you}\:\mathrm{add}\:\mathrm{some}\:\mathrm{discrete}\:\mathrm{entity}\:\mathrm{for}\:\mathrm{a}\:\mathrm{very}\:\mathrm{large} \\ $$$$\mathrm{number}\:\mathrm{you}\:\mathrm{put}\:\Sigma \\ $$$$\mathrm{like}\:\mathrm{if}\:\mathrm{you}\:\mathrm{add}\:\mathrm{all}\:\mathrm{the}\:\mathrm{natural}\:\mathrm{number}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to} \\ $$$$\infty\:\mathrm{you}\:\mathrm{put}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\mathrm{n}\:\mathrm{but}\:\mathrm{if}\:\mathrm{you}\:\mathrm{add}\:\mathrm{an}\:\mathrm{continuos}\:\mathrm{entity} \\ $$$$\mathrm{such}\:\mathrm{as}\:\mathrm{time}\:\mathrm{which}\:\mathrm{takes}\:\mathrm{all}\:\mathrm{the}\:\mathrm{values}\:\mathrm{in}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{you}\:\mathrm{use}\:\int \\ $$

Commented by Ar Brandon last updated on 02/May/20

$$\mathrm{OK}\:\mathrm{got}\:\mathrm{it}!\:\mathrm{Thanks} \\ $$

Commented by mathmax by abdo last updated on 02/May/20

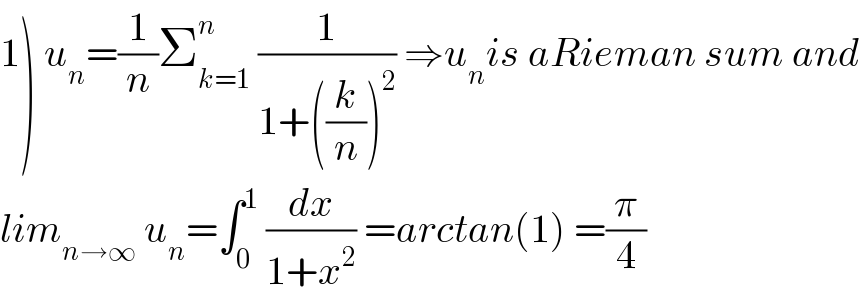
1) u_n =(1/n)Σ_(k=1) ^n (1/(1+((k/n))^2 )) ⇒u_n is aRieman sum and lim_(n→∞) u_n =∫_0 ^1 (dx/(1+x^2 )) =arctan(1) =(π/4)

$$\left.\mathrm{1}\right)\:{u}_{{n}} =\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }\:\Rightarrow{u}_{{n}} {is}\:{aRieman}\:{sum}\:{and}\: \\ $$$${lim}_{{n}\rightarrow\infty} \:{u}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={arctan}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{4}} \\ $$

Facebook Tweet Pin

find-the-limits-of-1-u-n-k-1-n-n-n-2-k-2-2-v-n-k-1-n-1-n-2-2kn-

Leave a Reply Cancel reply