Find-the-locus-of-a-point-which-moves-such-that-its-distance-from-the-line-y-4-is-a-constant-k-

Question Number 83570 by TawaTawa1 last updated on 03/Mar/20

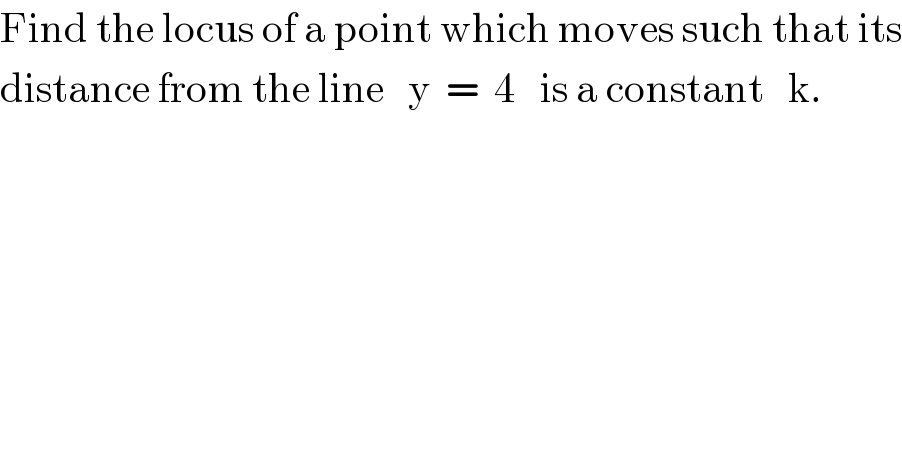
Find the locus of a point which moves such that its

distance from the line y = 4 is a constant k .

Commented by TawaTawa1 last updated on 03/Mar/20

Please help .

Commented by MJS last updated on 03/Mar/20

this is easy . scetch it . the line y = 4 is horizontal

{we}^{'} re searching all points with distance k from

this line . these are located on 2 horizontal

lines : y = 4 \pm k

Commented by TawaTawa1 last updated on 04/Mar/20

God bless you sir .

Answered by mr W last updated on 04/Mar/20

t h e l o c u s o f a p o i n t w h i c h h a s a

c o n s t a n t d i s t a n c e t o a g i v e n l i n e

i s a c y l i n d e r w h o s e a x i s i s t h e g i v e n

l i n e a n d w h o s e r a d i u s i s t h e g i v e n

d i s t a n c e .

Commented by TawaTawa1 last updated on 04/Mar/20

God bless you sir .

Answered by mind is power last updated on 03/Mar/20

l e t Y = f (x) b e e e q u a t i o n o f c o u r b e w e r r e t b i s p o i n t m o v e s

\Rightarrow D ((x, f (x)), Y = 4)

D ((x_{1}, y_{1}), a x + b y + c = 0) = \frac{∣ {a x}_{1} + {b y}_{1} + c ∣}{\sqrt{a^{2} + b^{2}}}

= \frac{∣ f (x) - 4 ∣}{1} =∣ f (x) - 4 ∣= k

\Rightarrow {\begin{cases} f (x) = k + 4 \\ f (x) = 4 - k \end{cases}

\Rightarrow f (x) = c

\Rightarrow M \in {(x, k)}

M \in L i g n w i t h e e q u a t i o n Y = c, c o n s t a n t e

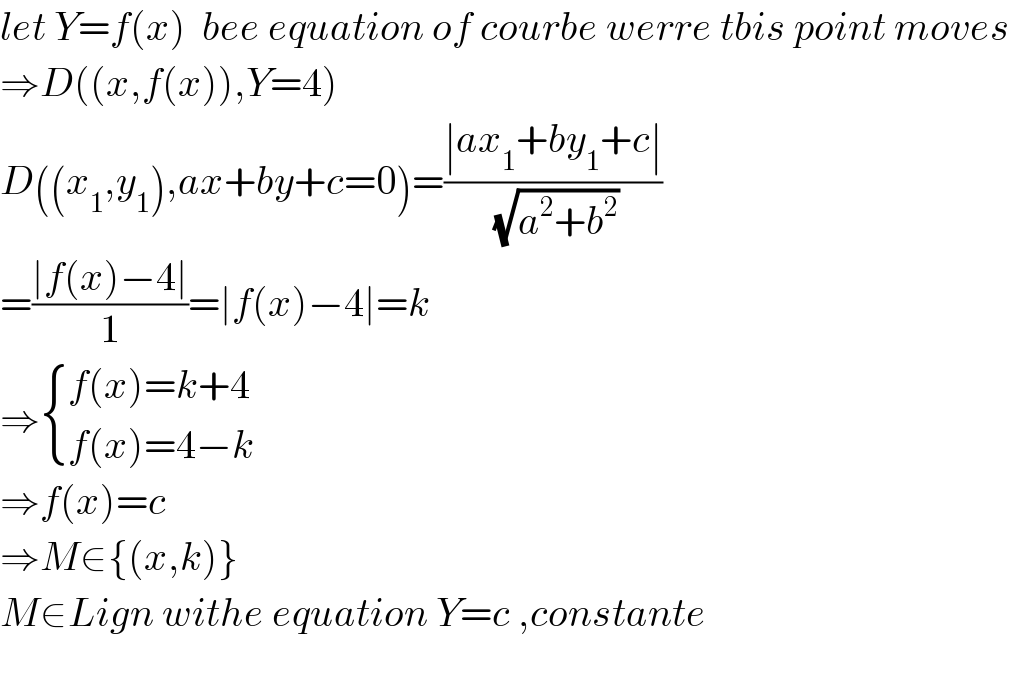
Commented by jagoll last updated on 03/Mar/20

sir please q 83513

Commented by TawaTawa1 last updated on 04/Mar/20

God bless you sir