Question Number 111284 by Aina Samuel Temidayo last updated on 03/Sep/20

Commented by mr W last updated on 03/Sep/20
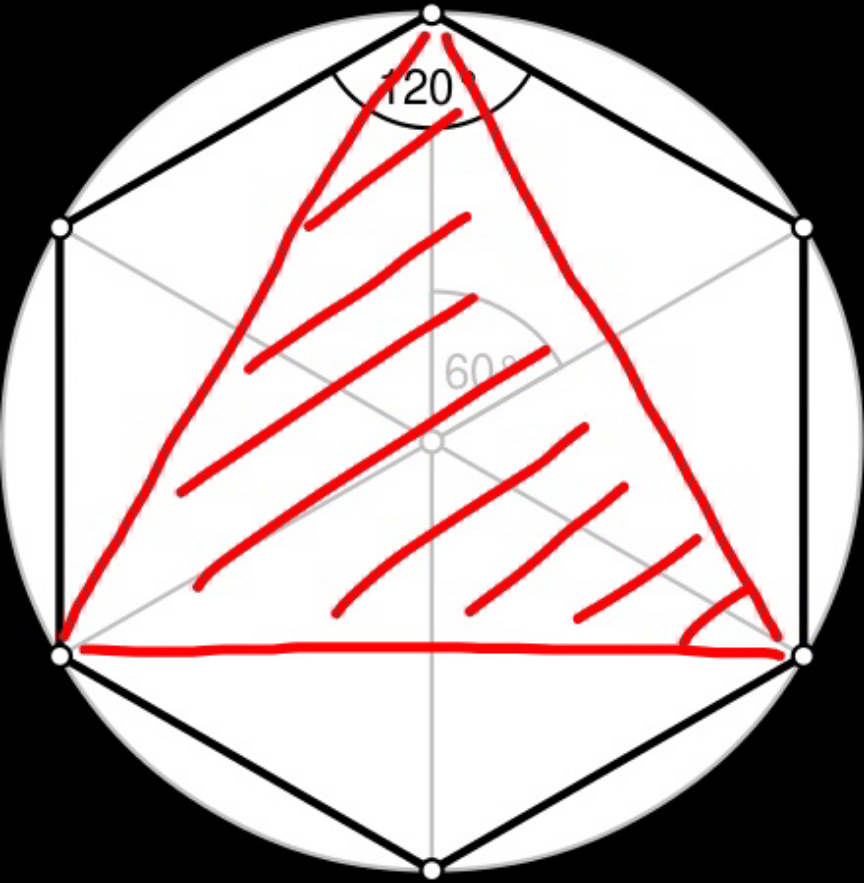
Commented by mr W last updated on 03/Sep/20
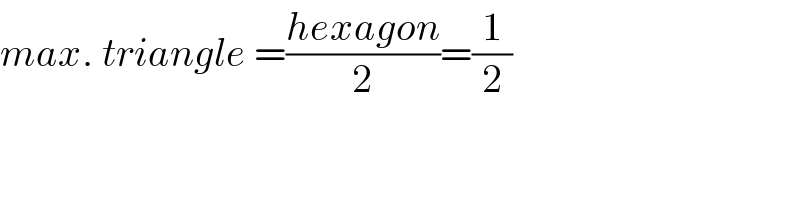
Commented by Aina Samuel Temidayo last updated on 03/Sep/20

Commented by Aina Samuel Temidayo last updated on 03/Sep/20
Commented by Her_Majesty last updated on 03/Sep/20

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

Commented by mr W last updated on 03/Sep/20
Commented by Her_Majesty last updated on 03/Sep/20
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
Commented by Aina Samuel Temidayo last updated on 03/Sep/20

Commented by Her_Majesty last updated on 03/Sep/20

