Menu Close

Find-the-maximum-distance-between-two-points-on-the-curve-x-4-a-4-y-4-b-4-1-

Tinku Tara 0 Comments
Pin




Question Number 144995 by liberty last updated on 01/Jul/21
Find the maximum distance between two points on the curve (x^4 /a^4 ) + (y^4 /b^4 ) = 1 .
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{distance}\: \\ $$$$\mathrm{between}\:\mathrm{two}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the}\: \\ $$$$\:\mathrm{curve}\:\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{4}} }\:+\:\frac{\mathrm{y}^{\mathrm{4}} }{\mathrm{b}^{\mathrm{4}} }\:=\:\mathrm{1}\:. \\ $$
Answered by mr W last updated on 01/Jul/21
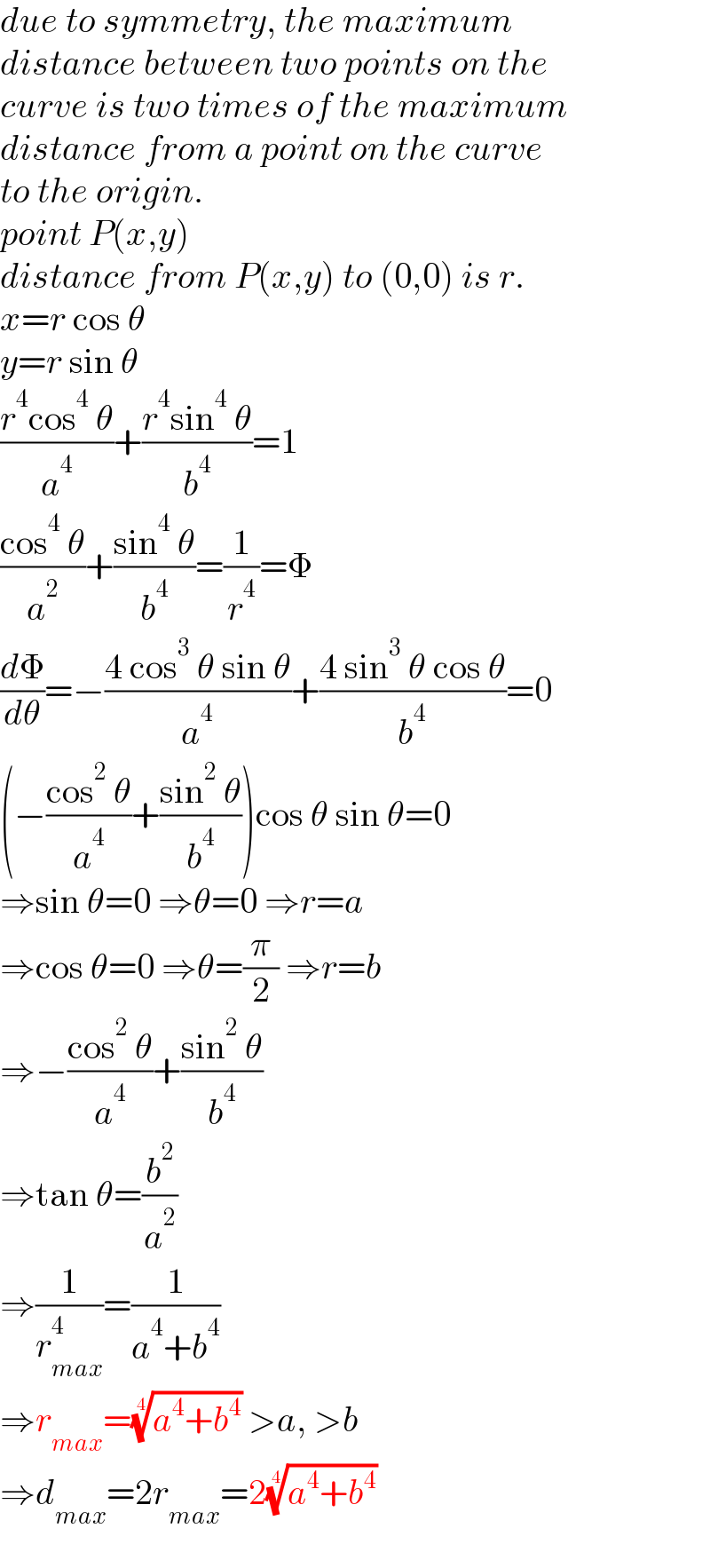
due to symmetry, the maximum distance between two points on the curve is two times of the maximum distance from a point on the curve to the origin. point P(x,y) distance from P(x,y) to (0,0) is r. x=r cos θ y=r sin θ ((r^4 cos^4 θ)/a^4 )+((r^4 sin^4 θ)/b^4 )=1 ((cos^4 θ)/a^2 )+((sin^4 θ)/b^4 )=(1/r^4 )=Φ (dΦ/dθ)=−((4 cos^3 θ sin θ)/a^4 )+((4 sin^3 θ cos θ)/b^4 )=0 (−((cos^2 θ)/a^4 )+((sin^2 θ)/b^4 ))cos θ sin θ=0 ⇒sin θ=0 ⇒θ=0 ⇒r=a ⇒cos θ=0 ⇒θ=(π/2) ⇒r=b ⇒−((cos^2 θ)/a^4 )+((sin^2 θ)/b^4 ) ⇒tan θ=(b^2 /a^2 ) ⇒(1/r_(max) ^4 )=(1/(a^4 +b^4 )) ⇒r_(max) =((a^4 +b^4 ))^(1/4) >a, >b ⇒d_(max) =2r_(max) =2((a^4 +b^4 ))^(1/4)
$${due}\:{to}\:{symmetry},\:{the}\:{maximum}\: \\ $$$${distance}\:{between}\:{two}\:{points}\:{on}\:{the} \\ $$$${curve}\:{is}\:{two}\:{times}\:{of}\:{the}\:{maximum} \\ $$$${distance}\:{from}\:{a}\:{point}\:{on}\:{the}\:{curve} \\ $$$${to}\:{the}\:{origin}. \\ $$$${point}\:{P}\left({x},{y}\right) \\ $$$${distance}\:{from}\:{P}\left({x},{y}\right)\:{to}\:\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{r}. \\ $$$${x}={r}\:\mathrm{cos}\:\theta \\ $$$${y}={r}\:\mathrm{sin}\:\theta \\ $$$$\frac{{r}^{\mathrm{4}} \mathrm{cos}^{\mathrm{4}} \:\theta}{{a}^{\mathrm{4}} }+\frac{{r}^{\mathrm{4}} \mathrm{sin}^{\mathrm{4}} \:\theta}{{b}^{\mathrm{4}} }=\mathrm{1} \\ $$$$\frac{\mathrm{cos}^{\mathrm{4}} \:\theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}^{\mathrm{4}} \:\theta}{{b}^{\mathrm{4}} }=\frac{\mathrm{1}}{{r}^{\mathrm{4}} }=\Phi \\ $$$$\frac{{d}\Phi}{{d}\theta}=−\frac{\mathrm{4}\:\mathrm{cos}^{\mathrm{3}} \:\theta\:\mathrm{sin}\:\theta}{{a}^{\mathrm{4}} }+\frac{\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\theta\:\mathrm{cos}\:\theta}{{b}^{\mathrm{4}} }=\mathrm{0} \\ $$$$\left(−\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{4}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{4}} }\right)\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\mathrm{0}\:\Rightarrow\theta=\mathrm{0}\:\Rightarrow{r}={a} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\mathrm{0}\:\Rightarrow\theta=\frac{\pi}{\mathrm{2}}\:\Rightarrow{r}={b} \\ $$$$\Rightarrow−\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{4}} }+\frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{4}} } \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{r}_{{max}} ^{\mathrm{4}} }=\frac{\mathrm{1}}{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} } \\ $$$$\Rightarrow{r}_{{max}} =\sqrt[{\mathrm{4}}]{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\:>{a},\:>{b} \\ $$$$\Rightarrow{d}_{{max}} =\mathrm{2}{r}_{{max}} =\mathrm{2}\sqrt[{\mathrm{4}}]{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} } \\ $$
Commented by mr W last updated on 01/Jul/21

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *