Menu Close

Find-the-maximum-of-f-x-cos-x-tan-x-1-tan-x-sin-x-in-terms-of-with-gt-1-and-0-lt-x-lt-tan-1-

Tinku Tara 0 Comments
Pin




Question Number 48739 by mr W last updated on 28/Nov/18
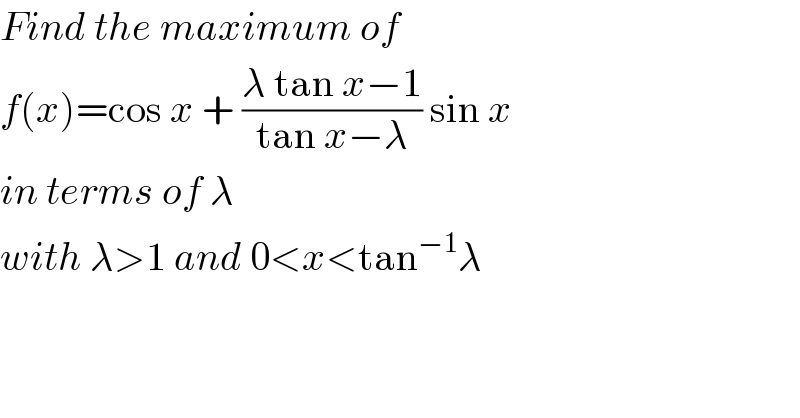
Find the maximum of f(x)=cos x + ((λ tan x−1)/(tan x−λ)) sin x in terms of λ with λ>1 and 0<x<tan^(−1) λ
$${Find}\:{the}\:{maximum}\:{of} \\ $$$${f}\left({x}\right)=\mathrm{cos}\:{x}\:+\:\frac{\lambda\:\mathrm{tan}\:{x}−\mathrm{1}}{\mathrm{tan}\:{x}−\lambda}\:\mathrm{sin}\:{x} \\ $$$${in}\:{terms}\:{of}\:\lambda \\ $$$${with}\:\lambda>\mathrm{1}\:{and}\:\mathrm{0}<{x}<\mathrm{tan}^{−\mathrm{1}} \lambda \\ $$
Answered by MJS last updated on 28/Nov/18
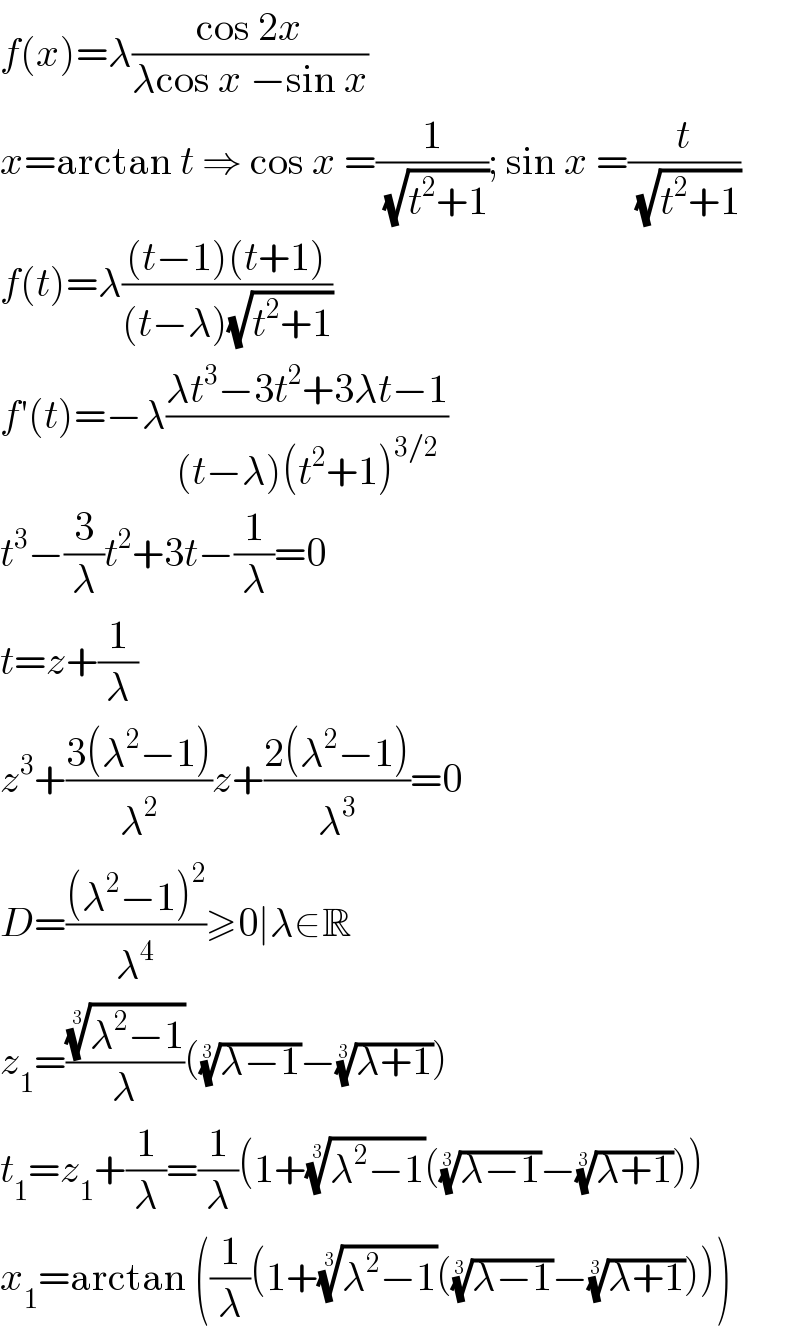
f(x)=λ((cos 2x)/(λcos x −sin x)) x=arctan t ⇒ cos x =(1/( (√(t^2 +1)))); sin x =(t/( (√(t^2 +1)))) f(t)=λ(((t−1)(t+1))/((t−λ)(√(t^2 +1)))) f′(t)=−λ((λt^3 −3t^2 +3λt−1)/((t−λ)(t^2 +1)^(3/2) )) t^3 −(3/λ)t^2 +3t−(1/λ)=0 t=z+(1/λ) z^3 +((3(λ^2 −1))/λ^2 )z+((2(λ^2 −1))/λ^3 )=0 D=(((λ^2 −1)^2 )/λ^4 )≥0∣λ∈R z_1 =(((λ^2 −1))^(1/3) /λ)(((λ−1))^(1/3) −((λ+1))^(1/3) ) t_1 =z_1 +(1/λ)=(1/λ)(1+((λ^2 −1))^(1/3) (((λ−1))^(1/3) −((λ+1))^(1/3) )) x_1 =arctan ((1/λ)(1+((λ^2 −1))^(1/3) (((λ−1))^(1/3) −((λ+1))^(1/3) )))
$${f}\left({x}\right)=\lambda\frac{\mathrm{cos}\:\mathrm{2}{x}}{\lambda\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}} \\ $$$${x}=\mathrm{arctan}\:{t}\:\Rightarrow\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}};\:\mathrm{sin}\:{x}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${f}\left({t}\right)=\lambda\frac{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{\left({t}−\lambda\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${f}'\left({t}\right)=−\lambda\frac{\lambda{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}\lambda{t}−\mathrm{1}}{\left({t}−\lambda\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{3}}{\lambda}{t}^{\mathrm{2}} +\mathrm{3}{t}−\frac{\mathrm{1}}{\lambda}=\mathrm{0} \\ $$$${t}={z}+\frac{\mathrm{1}}{\lambda} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{3}\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)}{\lambda^{\mathrm{2}} }{z}+\frac{\mathrm{2}\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)}{\lambda^{\mathrm{3}} }=\mathrm{0} \\ $$$${D}=\frac{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\lambda^{\mathrm{4}} }\geqslant\mathrm{0}\mid\lambda\in\mathbb{R} \\ $$$${z}_{\mathrm{1}} =\frac{\sqrt[{\mathrm{3}}]{\lambda^{\mathrm{2}} −\mathrm{1}}}{\lambda}\left(\sqrt[{\mathrm{3}}]{\lambda−\mathrm{1}}−\sqrt[{\mathrm{3}}]{\lambda+\mathrm{1}}\right) \\ $$$${t}_{\mathrm{1}} ={z}_{\mathrm{1}} +\frac{\mathrm{1}}{\lambda}=\frac{\mathrm{1}}{\lambda}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\lambda^{\mathrm{2}} −\mathrm{1}}\left(\sqrt[{\mathrm{3}}]{\lambda−\mathrm{1}}−\sqrt[{\mathrm{3}}]{\lambda+\mathrm{1}}\right)\right) \\ $$$${x}_{\mathrm{1}} =\mathrm{arctan}\:\left(\frac{\mathrm{1}}{\lambda}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\lambda^{\mathrm{2}} −\mathrm{1}}\left(\sqrt[{\mathrm{3}}]{\lambda−\mathrm{1}}−\sqrt[{\mathrm{3}}]{\lambda+\mathrm{1}}\right)\right)\right) \\ $$
Commented by mr W last updated on 28/Nov/18
thank you sir! it′s correct and perfect! great job!
$${thank}\:{you}\:{sir}! \\ $$$${it}'{s}\:{correct}\:{and}\:{perfect}!\:{great}\:{job}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *