find-the-maximum-value-of-sin-2018-x-cos-2019-x-

Question Number 65345 by KanhAshish last updated on 28/Jul/19

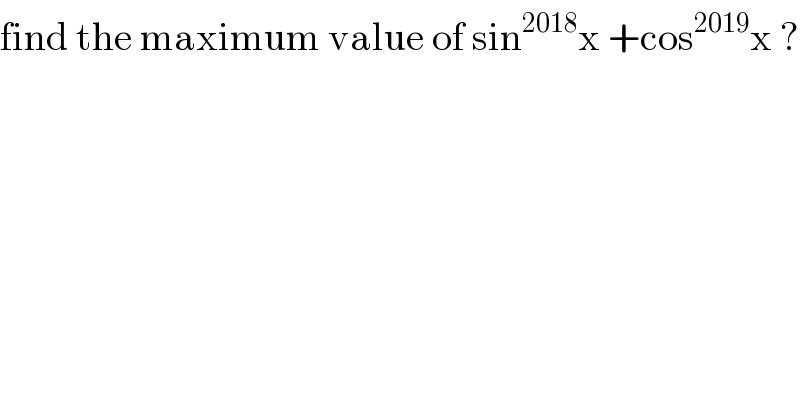
$$\mathrm{find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}^{\mathrm{2018}} \mathrm{x}\:+\mathrm{cos}^{\mathrm{2019}} \mathrm{x}\:? \\ $$

Commented by mr W last updated on 28/Jul/19

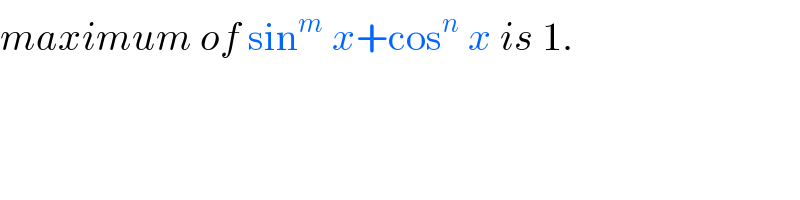
$${maximum}\:{of}\:\mathrm{sin}^{{m}} \:{x}+\mathrm{cos}^{{n}} \:{x}\:{is}\:\mathrm{1}. \\ $$

Commented by KanhAshish last updated on 28/Jul/19

$$\mathrm{how}?? \\ $$

Commented by KanhAshish last updated on 29/Jul/19

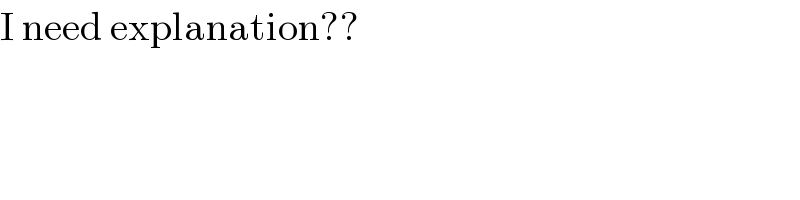
$$\mathrm{I}\:\mathrm{need}\:\mathrm{explanation}?? \\ $$

Commented by mr W last updated on 29/Jul/19

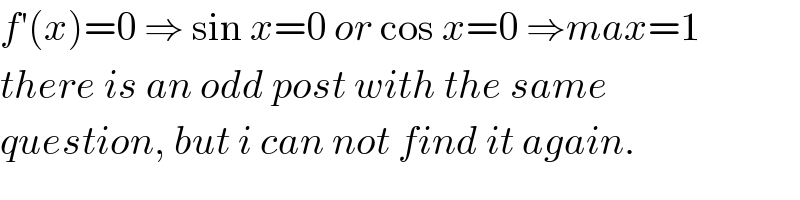
f′(x)=0 ⇒ sin x=0 or cos x=0 ⇒max=1 there is an odd post with the same question, but i can not find it again.

$${f}'\left({x}\right)=\mathrm{0}\:\Rightarrow\:\mathrm{sin}\:{x}=\mathrm{0}\:{or}\:\mathrm{cos}\:{x}=\mathrm{0}\:\Rightarrow{max}=\mathrm{1} \\ $$$${there}\:{is}\:{an}\:{odd}\:{post}\:{with}\:{the}\:{same} \\ $$$${question},\:{but}\:{i}\:{can}\:{not}\:{find}\:{it}\:{again}. \\ $$

Answered by MJS last updated on 29/Jul/19

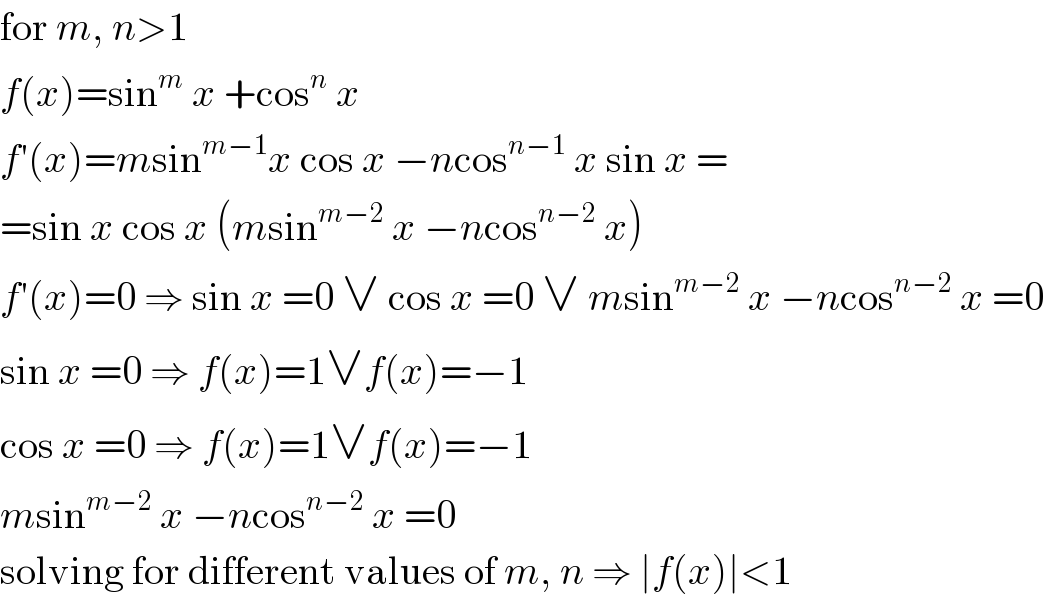
for m, n>1 f(x)=sin^m x +cos^n x f′(x)=msin^(m−1) x cos x −ncos^(n−1) x sin x = =sin x cos x (msin^(m−2) x −ncos^(n−2) x) f′(x)=0 ⇒ sin x =0 ∨ cos x =0 ∨ msin^(m−2) x −ncos^(n−2) x =0 sin x =0 ⇒ f(x)=1∨f(x)=−1 cos x =0 ⇒ f(x)=1∨f(x)=−1 msin^(m−2) x −ncos^(n−2) x =0 solving for different values of m, n ⇒ ∣f(x)∣<1

$$\mathrm{for}\:{m},\:{n}>\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{sin}^{{m}} \:{x}\:+\mathrm{cos}^{{n}} \:{x} \\ $$$${f}'\left({x}\right)={m}\mathrm{sin}^{{m}−\mathrm{1}} {x}\:\mathrm{cos}\:{x}\:−{n}\mathrm{cos}^{{n}−\mathrm{1}} \:{x}\:\mathrm{sin}\:{x}\:= \\ $$$$=\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:\left({m}\mathrm{sin}^{{m}−\mathrm{2}} \:{x}\:−{n}\mathrm{cos}^{{n}−\mathrm{2}} \:{x}\right) \\ $$$${f}'\left({x}\right)=\mathrm{0}\:\Rightarrow\:\mathrm{sin}\:{x}\:=\mathrm{0}\:\vee\:\mathrm{cos}\:{x}\:=\mathrm{0}\:\vee\:{m}\mathrm{sin}^{{m}−\mathrm{2}} \:{x}\:−{n}\mathrm{cos}^{{n}−\mathrm{2}} \:{x}\:=\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\:=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{1}\vee{f}\left({x}\right)=−\mathrm{1} \\ $$$$\mathrm{cos}\:{x}\:=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)=\mathrm{1}\vee{f}\left({x}\right)=−\mathrm{1} \\ $$$${m}\mathrm{sin}^{{m}−\mathrm{2}} \:{x}\:−{n}\mathrm{cos}^{{n}−\mathrm{2}} \:{x}\:=\mathrm{0} \\ $$$$\mathrm{solving}\:\mathrm{for}\:\mathrm{different}\:\mathrm{values}\:\mathrm{of}\:{m},\:{n}\:\Rightarrow\:\mid{f}\left({x}\right)\mid<\mathrm{1} \\ $$

Facebook Tweet Pin

find-the-maximum-value-of-sin-2018-x-cos-2019-x-

Leave a Reply Cancel reply