Find-the-minimum-value-of-f-x-9tan-2-4cot-2-

Question Number 50996 by rahul 19 last updated on 23/Dec/18

F i n d t h e m i n i m u m v a l u e o f

f (x) = {9 \tan}^{2} θ + {4 \cot}^{2} θ ?

Commented by rahul 19 last updated on 23/Dec/18

f (x) = {(3 \tan θ)}^{2} + {(2 \cot θ)}^{2} + 12 - 12

= {(3 t a n θ + 2 \cot θ)}^{2} - 12

\Rightarrow M i n i m u m V a l u e = - 12 .

Commented by rahul 19 last updated on 23/Dec/18

W h e r e a m i w r o n g ?

A n s i s + 12 .

Commented by mr W last updated on 23/Dec/18

f (x) = {(3 t a n θ + 2 \cot θ)}^{2} - 12 i s c o r r e c t,

b u t y o u c a n n o t s a y m i n i m u m o f f (x)

i s - 12, s i n c e t h e m i n i m u m o f

{(3 t a n θ + 2 \cot θ)}^{2} i s n o t z e r o! i n f a c t

t h e m i n i m u m o f {(3 t a n θ + 2 \cot θ)}^{2} i s 24,

t h e r e f o r e t h e m i n i m u m o f f (x) i s

24 - 12 = 12 . s o b e c a r e f u l w h e n u s i n g

t h e f o r m f (x) = {(\dots .)}^{2} + c, i t s m i n i n u m

i s c o n l y i f t h e m i n i m u m o f {(\dots .)}^{2} i s

z e r o! l o o k a t a n e x a m p l e :

f (x) = {(x^{2} + 2 x + 3)}^{2} - 1

i t s m i n i m u m i s n o t - 1, s i n c e m i n i m u m o f

{(x^{2} + 2 x + 3)}^{2} i s n o t z e r o, b u t 4, b e c a u s e

{(x^{2} + 2 x + 3)}^{2} = {[{(x + 1)}^{2} + 2]}^{2} ⩾ 2^{2} = 4 . i . e .

t h e m i n i m u m o f f (x) i s 3 .

t h e r e f o r e w h e n y o u a r e u s i n g

f (x) = {(\dots .)}^{2} + c, y o u s h o u l d a r r a n g e t h e

f o r m u l a i n t h e w a y t h a t {(\dots .)}^{2} c a n b e

z e r o, o n l y t h e n t h e m i n i m u m o f f (x)

i s c .

t h i s i s w h a t y o u h a v e h a d d o n e i n y o u r

e x a m p l e :

f (x) = {(3 \tan θ)}^{2} + {(2 \cot θ)}^{2} - 12 + 12

= {(3 t a n θ - 2 \cot θ)}^{2} + 12

\Rightarrow M i n i m u m V a l u e = 12 .

Commented by rahul 19 last updated on 23/Dec/18

S i r, h o w m i n . v a l u e o f

{(3 \tan θ + 2 \cot θ)}^{2} = 24 ?

Commented by mr W last updated on 23/Dec/18

{(3 x + \frac{2}{x})}^{2} ⩾ {(2 \sqrt{3 x \times \frac{2}{x}})}^{2} = {(2 \sqrt{6})}^{2} = 24

Commented by rahul 19 last updated on 23/Dec/18

T h a n k y o u S i r! :)

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

{(3 x + \frac{2}{x})}^{2} = {(3 x - \frac{2}{x})}^{2} + 4 \times 3 x \times \frac{2}{x}

{(3 x - \frac{2}{x})}^{2} a l w a y s + v e

s o f o r m i n {(3 x - \frac{2}{x})}^{2} = 0

h e n c e m i n v a l u e = 4 \times 3 x \times \frac{2}{x} = 24

Commented by 951172235v last updated on 04/Feb/19

A . M . ⩾ G . M .

\frac{9 \tan^{2} Θ + 4 \cot^{2} Θ}{2} ⩾ \sqrt{(9 \tan^{2} Θ) (4 \cot^{2} Θ)}

9 \tan^{2} Θ + 4 \cot^{2} Θ ⩾ 12

\min . of f (x) = 12

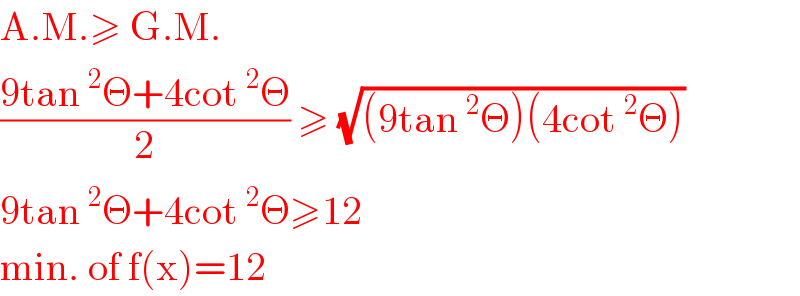
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

{(3 x)}^{2} + {(\frac{2}{x})}^{2}

= {(3 x - \frac{2}{x})}^{2} + 12

{(3 x - \frac{2}{x})}^{2} = a l a w a y s + v e

s o f (x) i s m i n i m u m w h e n {(3 x - \frac{2}{x})}^{2} = 0

3 x^{2} = 2 a t x = \pm \sqrt{\frac{2}{3}}

f (x) m i n v a l u e 12

Commented by rahul 19 last updated on 23/Dec/18

T h a n k y o u S i r!

Commented by tanmay.chaudhury50@gmail.com last updated on 23/Dec/18

m o s t w e l c o m e \dots