Question Number 26181 by NECx last updated on 21/Dec/17

$${Find}\:{the}\:{moment}\:{of}\:{inertia}\:{and} \\ $$$${the}\:{radius}\:{of}\:{gyration}\:{of}\:{a}\: \\ $$$${circular}\:{plate}\:{about}\:{an}\:{axis}\:{through} \\ $$$${its}\:{centre},{perpendicular}\:{to}\:{the} \\ $$$${plane}\:{of}\:{the}\:{plate}. \\ $$
Answered by mrW1 last updated on 22/Dec/17
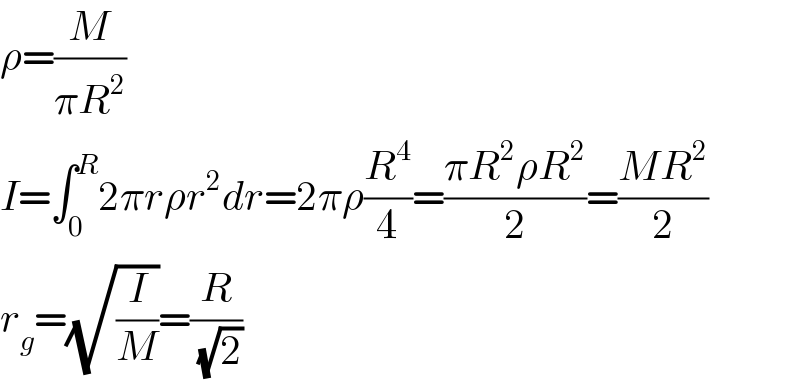
$$\rho=\frac{{M}}{\pi{R}^{\mathrm{2}} } \\ $$$${I}=\int_{\mathrm{0}} ^{{R}} \mathrm{2}\pi{r}\rho{r}^{\mathrm{2}} {dr}=\mathrm{2}\pi\rho\frac{{R}^{\mathrm{4}} }{\mathrm{4}}=\frac{\pi{R}^{\mathrm{2}} \rho{R}^{\mathrm{2}} }{\mathrm{2}}=\frac{{MR}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${r}_{{g}} =\sqrt{\frac{{I}}{{M}}}=\frac{{R}}{\:\sqrt{\mathrm{2}}} \\ $$
Answered by ajfour last updated on 21/Dec/17
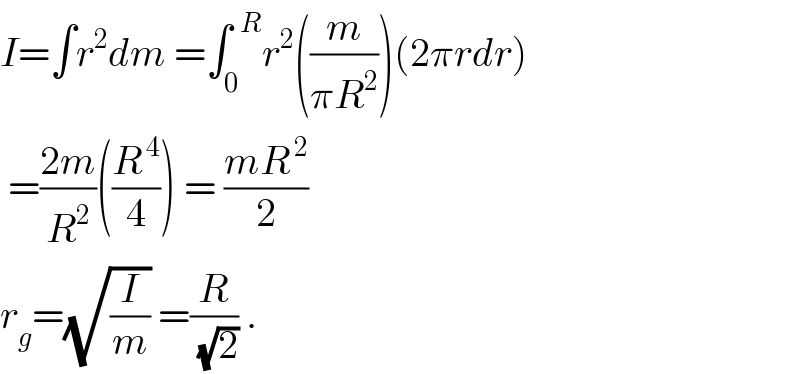
$${I}=\int{r}^{\mathrm{2}} {dm}\:=\int_{\mathrm{0}} ^{\:\:{R}} {r}^{\mathrm{2}} \left(\frac{{m}}{\pi{R}^{\mathrm{2}} }\right)\left(\mathrm{2}\pi{rdr}\right) \\ $$$$\:=\frac{\mathrm{2}{m}}{{R}^{\mathrm{2}} }\left(\frac{{R}^{\:\mathrm{4}} }{\mathrm{4}}\right)\:=\:\frac{{mR}^{\:\mathrm{2}} }{\mathrm{2}}\: \\ $$$${r}_{{g}} =\sqrt{\frac{{I}}{{m}}}\:=\frac{{R}}{\:\sqrt{\mathrm{2}}}\:. \\ $$
