Question Number 148418 by mathdanisur last updated on 27/Jul/21

$${Find}\:{the}\:{natural}\:{roots}\:{of}\:{the}\:{equation} \\ $$$${x}^{\mathrm{2}} \:-\:\mathrm{51}{y}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$
Answered by mr W last updated on 27/Jul/21
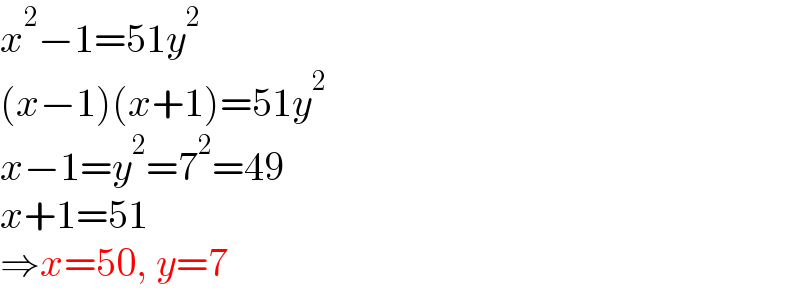
$${x}^{\mathrm{2}} −\mathrm{1}=\mathrm{51}{y}^{\mathrm{2}} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{51}{y}^{\mathrm{2}} \\ $$$${x}−\mathrm{1}={y}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} =\mathrm{49} \\ $$$${x}+\mathrm{1}=\mathrm{51} \\ $$$$\Rightarrow{x}=\mathrm{50},\:{y}=\mathrm{7} \\ $$
Commented by mathdanisur last updated on 27/Jul/21
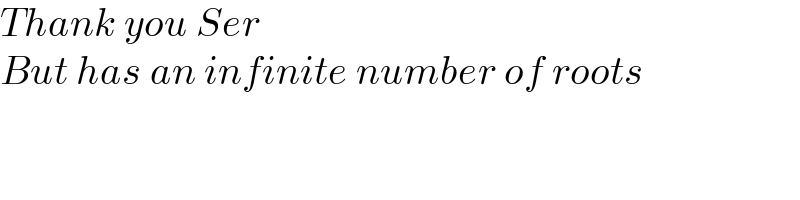
$${Thank}\:{you}\:{Ser} \\ $$$${But}\:{has}\:{an}\:{infinite}\:{number}\:{of}\:{roots} \\ $$
Commented by mr W last updated on 27/Jul/21
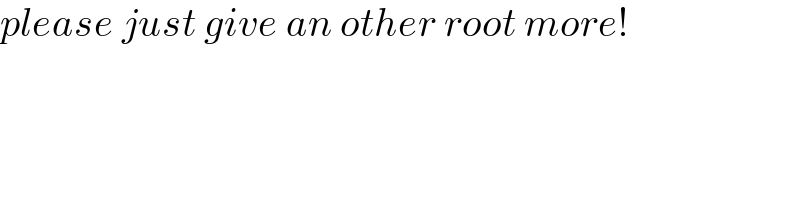
$${please}\:{just}\:{give}\:{an}\:{other}\:{root}\:{more}! \\ $$
Commented by mathdanisur last updated on 27/Jul/21

$${Ser},\:\left(\mathrm{499850}\:;\:\mathrm{69993}\right) \\ $$
Commented by mr W last updated on 27/Jul/21

$${thanks}! \\ $$
