Question Number 32932 by abdo imad last updated on 06/Apr/18
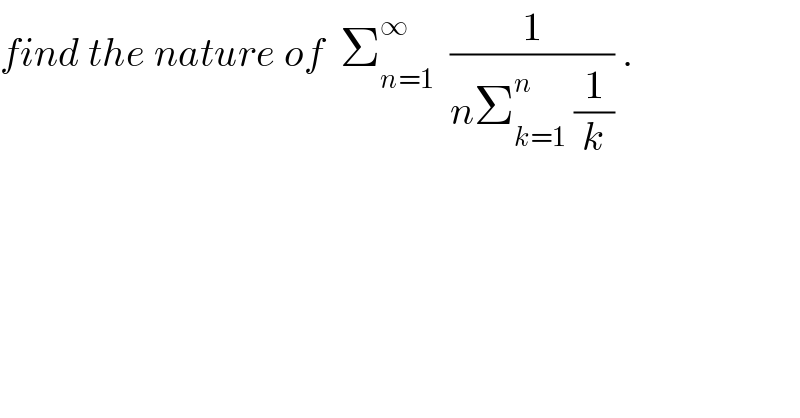
$${find}\:{the}\:{nature}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}}\:. \\ $$
Commented by prof Abdo imad last updated on 11/Apr/18
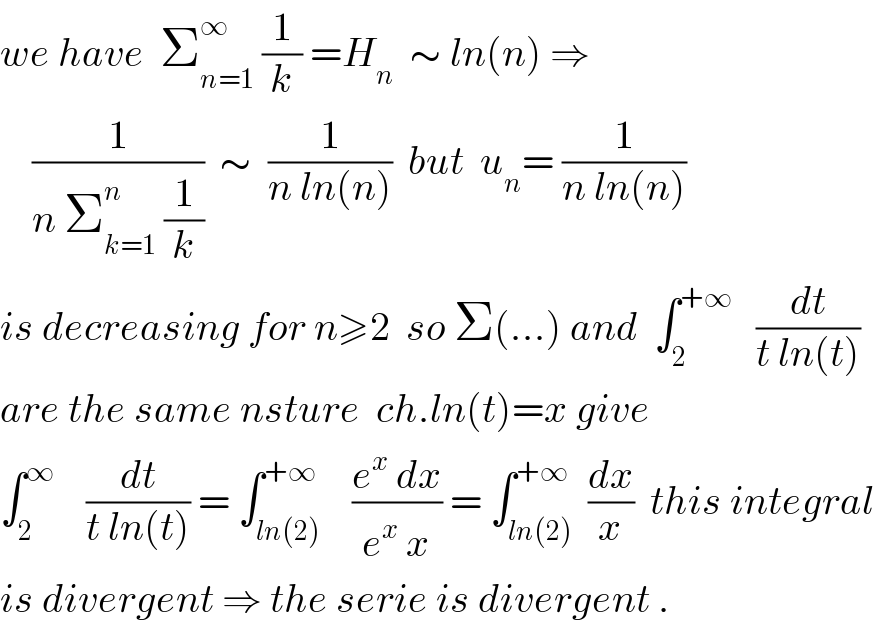
$${we}\:{have}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} \:\:\sim\:{ln}\left({n}\right)\:\Rightarrow \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{n}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}}\:\:\sim\:\:\frac{\mathrm{1}}{{n}\:{ln}\left({n}\right)}\:\:{but}\:\:{u}_{{n}} =\:\frac{\mathrm{1}}{{n}\:{ln}\left({n}\right)} \\ $$$${is}\:{decreasing}\:{for}\:{n}\geqslant\mathrm{2}\:\:{so}\:\Sigma\left(…\right)\:{and}\:\:\int_{\mathrm{2}} ^{+\infty} \:\:\:\frac{{dt}}{{t}\:{ln}\left({t}\right)} \\ $$$${are}\:{the}\:{same}\:{nsture}\:\:{ch}.{ln}\left({t}\right)={x}\:{give} \\ $$$$\int_{\mathrm{2}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}\:{ln}\left({t}\right)}\:=\:\int_{{ln}\left(\mathrm{2}\right)} ^{+\infty} \:\:\:\frac{{e}^{{x}} \:{dx}}{{e}^{{x}} \:{x}}\:=\:\int_{{ln}\left(\mathrm{2}\right)} ^{+\infty} \:\frac{{dx}}{{x}}\:\:{this}\:{integral} \\ $$$${is}\:{divergent}\:\Rightarrow\:{the}\:{serie}\:{is}\:{divergent}\:. \\ $$
