Question Number 26402 by abdo imad last updated on 25/Dec/17
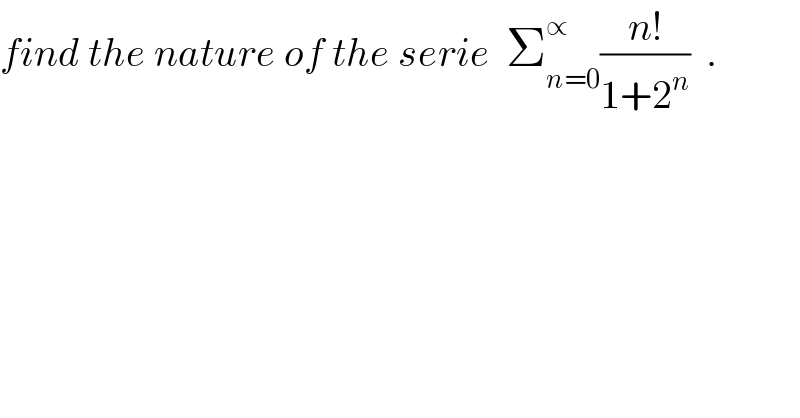
$${find}\:{the}\:{nature}\:{of}\:{the}\:{serie}\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \frac{{n}!}{\mathrm{1}+\mathrm{2}^{{n}} }\:\:. \\ $$
Commented by prakash jain last updated on 25/Dec/17

$${n}!=\mathrm{2}^{{n}−\mathrm{1}} .\underset{{j}=\mathrm{3}} {\overset{{n}} {\prod}}\left(\frac{{j}}{\mathrm{2}}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}!}{\mathrm{1}+\mathrm{2}^{{n}} }=\infty \\ $$
Commented by abdo imad last updated on 25/Dec/17
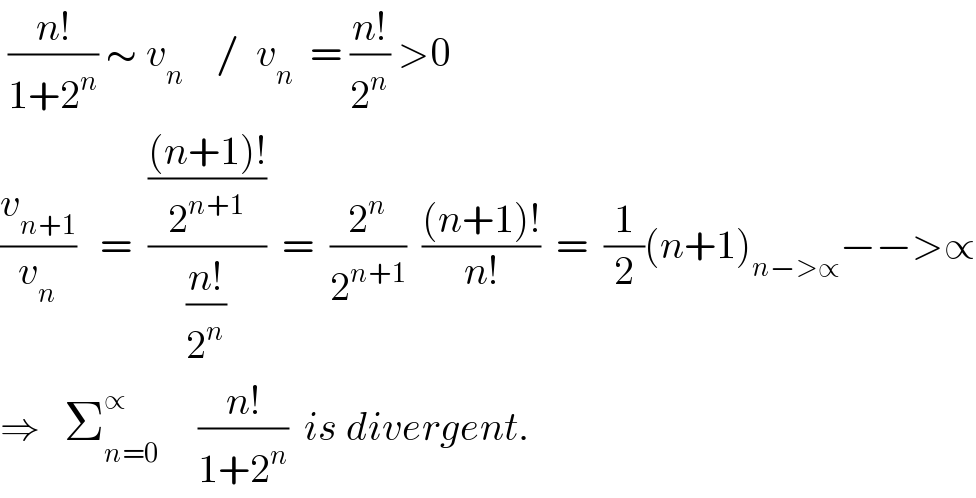
$$\:\frac{{n}!}{\mathrm{1}+\mathrm{2}^{{n}} }\:\sim\:{v}_{{n}} \:\:\:\:/\:\:{v}_{{n}} \:\:=\:\frac{{n}!}{\mathrm{2}^{{n}} }\:>\mathrm{0}\: \\ $$$$\frac{{v}_{{n}+\mathrm{1}} }{{v}_{{n}} }\:\:\:=\:\:\frac{\frac{\left({n}+\mathrm{1}\right)!}{\mathrm{2}^{{n}+\mathrm{1}} }}{\frac{{n}!}{\mathrm{2}^{{n}} }}\:\:=\:\:\frac{\mathrm{2}^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} }\:\:\frac{\left({n}+\mathrm{1}\right)!}{{n}!}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)_{{n}−>\propto} −−>\propto \\ $$$$\Rightarrow\:\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\:\:\:\frac{{n}!}{\mathrm{1}+\mathrm{2}^{{n}} }\:\:{is}\:{divergent}. \\ $$
Answered by prakash jain last updated on 25/Dec/17
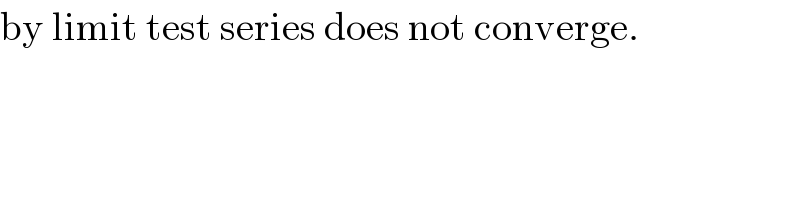
$$\mathrm{by}\:\mathrm{limit}\:\mathrm{test}\:\mathrm{series}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$
