find-the-next-4-term-and-the-n-th-term-1-2-5-26-

Question Number 28743 by Cheyboy last updated on 29/Jan/18

f i n d t h e n e x t 4 t e r m a n d t h e

n^{t h} t e r m

1, 2, 5, 26 \dots \dots .

Commented by Tinkutara last updated on 29/Jan/18

a_{n} = a_{n - 1}^{2} + 1

Commented by Cheyboy last updated on 29/Jan/18

t h a n k u s i r

Answered by ajfour last updated on 30/Jan/18

1, 2, 5, 26, 81, 186, 357, 610

1, 3, 21, 55, 105, 171, 253

2, 18, 34, 50, 66, 82

L e t t h e f i r s t s e r i e s 1, 2, 5, 26, \dots

b e T s e r i e s .

m i d d l e o n e S s e r i e s

l a s t o n e R s e r i e s

R_{n} = 2 + 16 (n - 1) = 16 n - 14

\underset{n = 1}{\sum^{n}} R_{n} = \underset{n = 1}{\sum^{n}} (S_{n + 1} - S_{n}) = \underset{n = 1}{\sum^{n}} (16 n - 14)

\Rightarrow S_{n + 1} - S_{1} = 8 n (n + 1) - 14 n

a s S_{1} = 1

S_{n + 1} = 8 n (n + 1) - 14 n + 1

S_{n + 1} = T_{n + 2} - T_{n + 1}

\Rightarrow \underset{n = 1}{\sum^{n}} (T_{n + 2} - T_{n + 1}) = \underset{n = 1}{\sum^{n}} [8 n (n + 1) - 14 n + 1]

= T_{n + 2} - T_{2} = \frac{8 n (n + 1) (n + 2)}{3} - 7 n (n + 1) + n

a s T_{2} = 2

T_{n + 2} = \frac{8 n (n + 1) (n + 2)}{3} - 7 n (n + 1)

+ n + 2

T_{n} = \frac{8 n (n - 1) (n - 2)}{3}

- 7 (n - 1) (n - 2) + n

= \frac{(n - 1) (n - 2) (8 n - 21)}{3} + n .

Commented by Cheyboy last updated on 29/Jan/18

t h a n k a l o t s i r

Commented by Cheyboy last updated on 29/Jan/18

s i r w h a t i s u r n^{t h}

Commented by Cheyboy last updated on 30/Jan/18

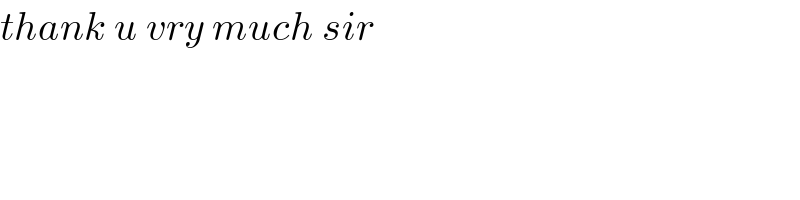
t h a n k u v r y m u c h s i r

Facebook Tweet Pin