Find-the-nth-term-of-the-sequence-a-n-such-that-a-1-a-2-a-n-n-n-1-n-n-1-2-3-

Question Number 98215 by I want to learn more last updated on 12/Jun/20

Find the nth term of the sequence {a_{n}} such that

\frac{a_{1} + a_{2} + \dots + a_{n}}{n} = n + \frac{1}{n} (n = 1, 2, 3, \dots)

Commented by Don08q last updated on 12/Jun/20

a_{1} + a_{2} + \dots + a_{n} = n (n + \frac{1}{n})

S_{n} = n (n + \frac{1}{n})

S_{n} = n^{2} + 1

\Rightarrow S_{n - 1} = {(n - 1)}^{2} + 1

The n t h term, a_{n} = S_{n} - S_{n - 1}

So, a_{n} = (n^{2} + 1) - (n^{2} - 2 n + 2)

∴ a_{n} = 2 n - 1

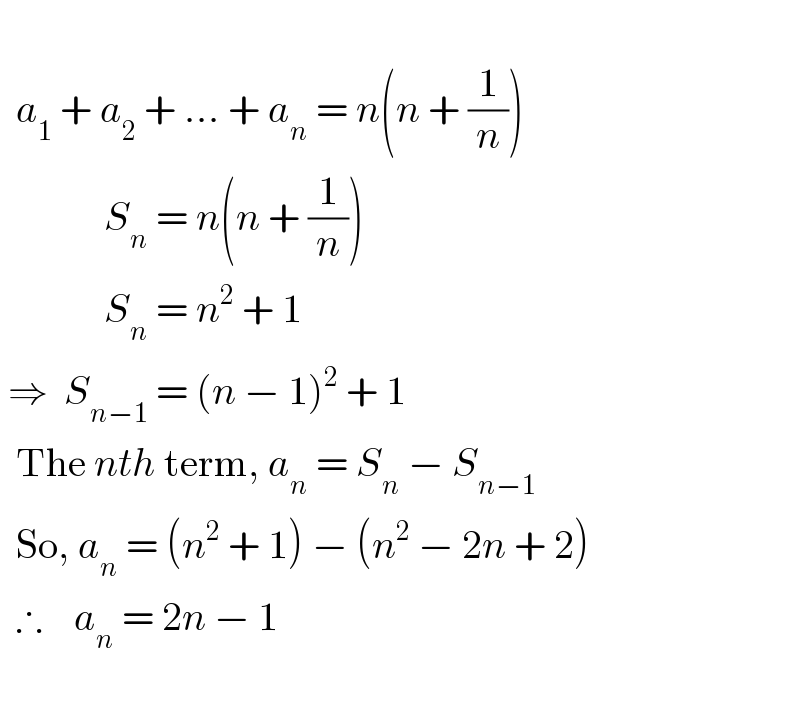
Commented by I want to learn more last updated on 12/Jun/20

Thanks sir

Answered by aadf last updated on 12/Jun/20

2 n - 1

Answered by mr W last updated on 12/Jun/20

\frac{S_{n}}{n} = n + \frac{1}{n} = \frac{n^{2} + 1}{n}

S_{n} = n^{2} + 1

S_{n - 1} = {(n - 1)}^{2} + 1

a_{n} = S_{n} - S_{n - 1} = n^{2} + 1 - {(n - 1)}^{2} - 1 = 2 n - 1

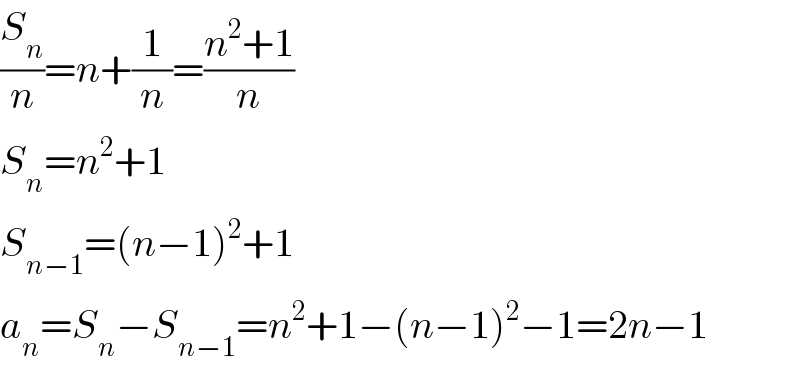
Commented by I want to learn more last updated on 12/Jun/20

Thanks sir

Answered by mathmax by abdo last updated on 12/Jun/20

\frac{a_{1} + a_{2} + \dots . + a_{n}}{n} = n + \frac{1}{n} \Rightarrow \sum_{k = 1}^{n} a_{k} = n^{2} + 1 \Rightarrow

\sum_{k = 1}^{n - 1} a_{k} = {(n - 1)}^{2} + 1 \Rightarrow \sum_{k = 1}^{n} a_{k} - \sum_{k = 1}^{n - 1} a_{k} = n^{2} - {(n - 1)}^{2} \Rightarrow

a_{n} = n^{2} - (n^{2} - 2 n + 1) = 2 n - 1

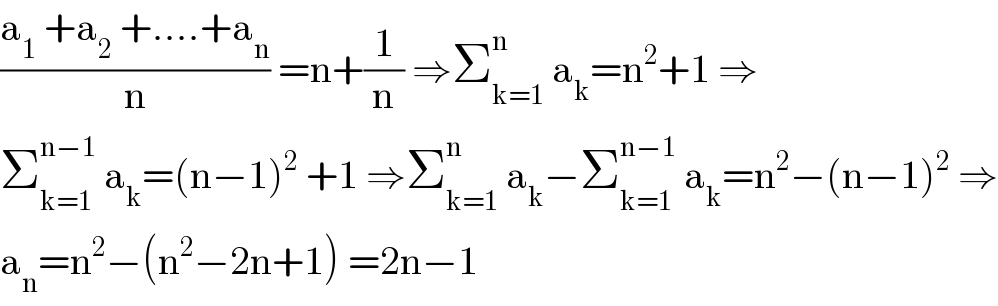
Commented by mathmax by abdo last updated on 12/Jun/20

you are welcome

Commented by I want to learn more last updated on 12/Jun/20

Thanks sir