find-the-number-of-5-digit-natural-numbers-with-strictly-ascending-digits-whose-sum-is-20-example-12458-is-such-a-number-

Question Number 188362 by mr W last updated on 28/Feb/23

f i n d t h e n u m b e r o f 5 d i g i t n a t u r a l

n u m b e r s w i t h s t r i c t l y a s c e n d i n g

d i g i t s w h o s e s u m i s 20 .

e x a m p l e : 12458 i s s u c h a n u m b e r

Answered by ARUNG_Brandon_MBU last updated on 28/Feb/23

6

Commented by ARUNG_Brandon_MBU last updated on 28/Feb/23

#include <iostream> using namespace std; int main(void) { for (int i0, i1, i2, i3, i4, i=10000; i<100000; i++) { i0 = i/10000; i1 = i%10000/1000; i2 = i%1000/100; i3 = i%100/10; i4 = i%10; if (i0<i1 && i1<i2 && i2<i3 && i3<i4) if ((i0+i1+i2+i3+i4) == 20) cout << i <<", "; } return 0; }

Commented by ARUNG_Brandon_MBU last updated on 28/Feb/23

Output: 12359, 12368, 12458, 12467, 13457, 23456,

Output : 12359, 12368, 12458,

12467, 13457, 23456,

Commented by mr W last updated on 28/Feb/23

y e s!

Commented by ARUNG_Brandon_MBU last updated on 28/Feb/23

��

Commented by mr W last updated on 01/Mar/23

in this case, i mean when the sum of digits is ≤20, we can still have a smart solution, which gives us the answer 7−1=6. 7 is the coef. of term x^(20) in the expansion Π_(k=1) ^5 (x^k /(1−x^k )). but it includes also the case that a digit is 10, which is certainly not true, therefore the correct answer is 7−1=6. if the sum of digits is >20, i think we can only enumerate all possible possibilities as your program does. there is no smarter approach.

i n t h i s c a s e, i m e a n w h e n t h e s u m o f

d i g i t s i s ⩽ 20, w e c a n s t i l l h a v e a

s m a r t s o l u t i o n, w h i c h g i v e s u s t h e

a n s w e r 7 - 1 = 6 .

7 i s t h e c o e f . o f t e r m x^{20} i n t h e

e x p a n s i o n \underset{k = 1}{\prod^{5}} \frac{x^{k}}{1 - x^{k}} . b u t i t i n c l u d e s

a l s o t h e c a s e t h a t a d i g i t i s 10, w h i c h

i s c e r t a i n l y n o t t r u e, t h e r e f o r e t h e

c o r r e c t a n s w e r i s 7 - 1 = 6 .

i f t h e s u m o f d i g i t s i s > 20, i t h i n k

w e c a n o n l y e n u m e r a t e a l l p o s s i b l e

p o s s i b i l i t i e s a s y o u r p r o g r a m d o e s .

t h e r e i s n o s m a r t e r a p p r o a c h .

Commented by ARUNG_Brandon_MBU last updated on 28/Feb/23

��

Commented by mr W last updated on 04/Mar/23

i found a new way even for n>20, see below. can you please check with your program?

i f o u n d a n e w w a y e v e n f o r n > 20,

s e e b e l o w . c a n y o u p l e a s e c h e c k w i t h

y o u r p r o g r a m ?

Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23

// for n > 20 #include <iostream> using namespace std; int main(void) { for(int i0,i1,i2,i3,i4,i=10000;i<100000;i++) { i0 = i/10000; i1 = i%10000/1000; i2 = i%1000/100; i3 = i%100/10; i4 = i%10; if (i0<i1 && i1<i2 && i2<i3 && i3<i4) if (i0+i1+i2+i3+i4 > 20) cout << i <<" "; } return 0; }

Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23

Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23

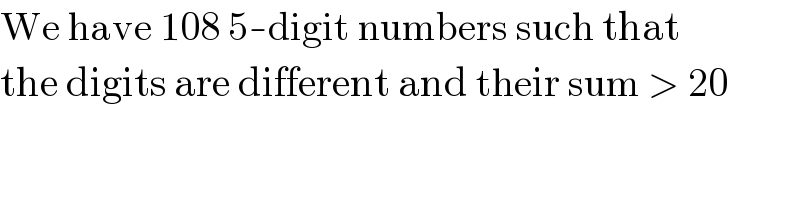
We have 108 5-digit numbers such that the digits are different and their sum > 20

We have 108 5 - digit numbers such that

the digits are different and their sum > 20

Commented by mr W last updated on 07/Mar/23

yes, that′s correct! as we can see below there are 8 numbers with sum 21, 9 numbers with sum 22, 11 numbers with sum 23, ... 2 numbers with sum 33, 1 number with sum 34, 1 number with sum 35. so totally 108 numbers with sum>20.

y e s, {t h a t}^{'} s c o r r e c t!

a s w e c a n s e e b e l o w t h e r e a r e

8 n u m b e r s w i t h s u m 21,

9 n u m b e r s w i t h s u m 22,

11 n u m b e r s w i t h s u m 23,

\dots

2 n u m b e r s w i t h s u m 33,

1 n u m b e r w i t h s u m 34,

1 n u m b e r w i t h s u m 35 .

s o t o t a l l y 108 n u m b e r s w i t h s u m > 20 .

Answered by mr W last updated on 04/Mar/23

a new try say the number is d_1 d_2 d_3 d_4 d_5 with d_1 +d_2 +d_3 +d_4 +d_5 =n and 1≤d_1 <d_2 <d_3 <d_4 <d_5 ≤9 let d_1 =1+k_1 with 0≤k_1 ≤8 d_2 =d_1 +1+k_2 =2+k_1 +k_2 with 0≤k_2 ≤7 d_3 =d_2 +1+k_3 =3+k_1 +k_2 +k_3 with 0≤k_3 ≤6 ...... d_5 =d_4 +1+k_4 =5+k_1 +k_2 +k_3 +...+k_5 with 0≤k_3 ≤4 (1+2+3+...+5)+5k_1 +4k_2 +3k_3 +2k_4 +k_5 =n number of solutions is the coef. of term x^n in the expansion of x^(15) Π_(r=1) ^5 ((1−x^(10−r) )/(1−x^r )) for n=20 we have 6 numbers and for n=25 we have 12 numbers etc.

a n e w t r y

s a y t h e n u m b e r i s d_{1} d_{2} d_{3} d_{4} d_{5} w i t h

d_{1} + d_{2} + d_{3} + d_{4} + d_{5} = n a n d

1 ⩽ d_{1} < d_{2} < d_{3} < d_{4} < d_{5} ⩽ 9

l e t

d_{1} = 1 + k_{1} w i t h 0 ⩽ k_{1} ⩽ 8

d_{2} = d_{1} + 1 + k_{2} = 2 + k_{1} + k_{2} w i t h 0 ⩽ k_{2} ⩽ 7

d_{3} = d_{2} + 1 + k_{3} = 3 + k_{1} + k_{2} + k_{3} w i t h 0 ⩽ k_{3} ⩽ 6

\dots \dots

d_{5} = d_{4} + 1 + k_{4} = 5 + k_{1} + k_{2} + k_{3} + \dots + k_{5} w i t h 0 ⩽ k_{3} ⩽ 4

(1 + 2 + 3 + \dots + 5) + 5 k_{1} + 4 k_{2} + 3 k_{3} + 2 k_{4} + k_{5} = n

n u m b e r o f s o l u t i o n s i s t h e c o e f . o f

t e r m x^{n} i n t h e e x p a n s i o n o f

x^{15} \underset{r = 1}{\prod^{5}} \frac{1 - x^{10 - r}}{1 - x^{r}}

f o r n = 20 w e h a v e 6 n u m b e r s a n d

f o r n = 25 w e h a v e 12 n u m b e r s e t c .

Commented by mr W last updated on 04/Mar/23

Commented by mr W last updated on 04/Mar/23

in case of 6 digit numbers we need to find the coef. of term x^n in x^(21) Π_(r=1) ^6 ((1−x^(10−r) )/(1−x^r )) for n=25 we have 4 numbers and for n=30 we have 8 numbers etc.

i n c a s e o f 6 d i g i t n u m b e r s w e n e e d

t o f i n d t h e c o e f . o f t e r m x^{n} i n

x^{21} \underset{r = 1}{\prod^{6}} \frac{1 - x^{10 - r}}{1 - x^{r}}

f o r n = 25 w e h a v e 4 n u m b e r s a n d

f o r n = 30 w e h a v e 8 n u m b e r s e t c .

Commented by mr W last updated on 04/Mar/23

Facebook Tweet Pin

find-the-number-of-5-digit-natural-numbers-with-strictly-ascending-digits-whose-sum-is-20-example-12458-is-such-a-number-

Leave a Reply Cancel reply