Find-the-number-of-all-5-digit-numbers-x-1-x-2-x-3-x-4-x-5-with-x-1-x-2-x-3-x-4-x-5-

Question Number 117708 by mr W last updated on 13/Oct/20

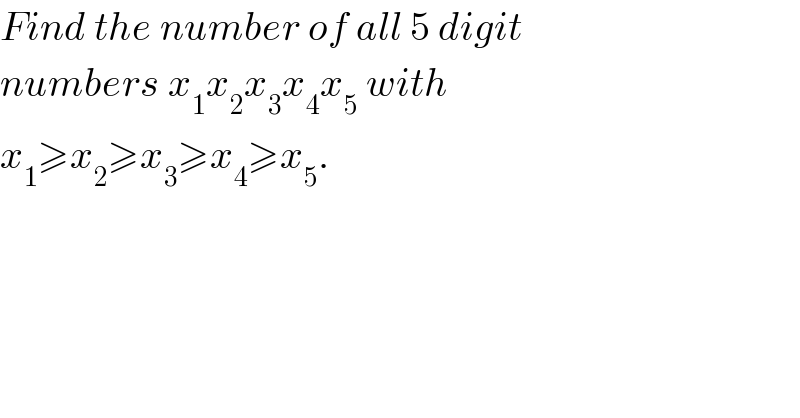
F i n d t h e n u m b e r o f a l l 5 d i g i t

n u m b e r s x_{1} x_{2} x_{3} x_{4} x_{5} w i t h

x_{1} ⩾ x_{2} ⩾ x_{3} ⩾ x_{4} ⩾ x_{5} .

Commented by prakash jain last updated on 13/Oct/20

(Σ_(j=0) ^4 ^4 C_j ×^(10) C_(j+1) )−1 ^4 C_j indicates partion of 5 into j+1 parts. ^(10) C_(j+1) way to choose j+1 digits. −1 to exclude all zero cases for n digits (Σ_(j=0) ^(n−1) ^(n−1) C_j ×^(10) C_(j+1) )−1

(\underset{j = 0}{\sum^{4}}^{4} C_{j} \times^{10} C_{j + 1}) - 1

^{4} C_{j} indicates partion of 5 into j + 1 parts .

^{10} C_{j + 1} way to choose j + 1 digits .

- 1 to exclude all zero cases

for n digits

(\underset{j = 0}{\sum^{n - 1}}^{n - 1} C_{j} \times^{10} C_{j + 1}) - 1

Commented by prakash jain last updated on 13/Oct/20

Distribution calculation 5 digits • • • • • We can 5 digits in j+1 number of part by placing j bar in space between dots. for a 5 digit number formed with 2 unique digits we have following ways 1d_1 +4d_2 =•∣•••• 1d_1 +4d_2 ,2d_1 +3d_2 ,3d_1 +2d_2 ,4d_1 +d_2 = ^4 C_1 there are^(10) C_2 ways to select 2 digits. similar for j digits ^4 C_j ways to decide which digit is repeated how many time. ^(10) C_j ways to select j digits. once we have selected digits and decided how many times each digit is repeated then there is only one unique way of writing sorted number. so numbers of way a 5 digit number can be written using j different digits in the required sorted order is. ^4 C_(j−1) ×^(10) C_j we need to subtract 1 for case where a single digit is repeated 5 times. so 5 digit numbers in required sorted order are 2001.

Distribution calculation

5 digits

∙ ∙ ∙ ∙ ∙

We can 5 digits in j + 1 number of

part by placing j bar in space between

dots .

for a 5 digit number formed with

2 unique digits we have following

ways

1 d_{1} + 4 d_{2} = ∙ ∣ ∙ ∙ ∙ ∙

{1 d}_{1} + {4 d}_{2}, 2 d_{1} + 3 d_{2}, 3 d_{1} + 2 d_{2}, 4 d_{1} + d_{2}

=^{4} C_{1}

there are^{10} C_{2} ways to select 2 digits .

similar for j digits

^{4} C_{j} ways to decide which digit is repeated

how many time .

^{10} C_{j} ways to select j digits .

once we have selected digits

and decided how many times

each digit is repeated then

there is only one unique way of

writing sorted number .

so numbers of way a 5 digit number

can be written using j different digits

in the required sorted order is .

^{4} C_{j - 1} \times^{10} C_{j}

we need to subtract 1 for case where

a single digit is repeated 5 times .

so 5 digit numbers in required

sorted order are 2001 .

Commented by mr W last updated on 13/Oct/20

n i c e s o l u t i o n s i r!

Answered by 1549442205PVT last updated on 14/Oct/20

For convenient we write abcde^(−) instead of x_1 x_2 x_3 x_4 x_5 ^(−) and ∣abcde∣−number of numbers of form abcde^(−) We solve the problem in turn for cases 1)How many are there the two−digit numbers ab^(−) can be formed from the digits 1,..,9 such that a≥b This case,it is easy to see in the total we can establish p=C_9 ^2 +9=45 ones 2)The case abc^(−) . When 9 at first place we have C_8 ^2 +8+9=45 numbers of form 9bc^(−) Similarly,∣8bc^(−) ∣= C_7 ^2 +7+8=36 ones ,.....,∣5bc^(−) ∣=C_4 ^2 +4+5=15 ones ∣4bc^(−) ∣=C_3 ^2 +3+4=10;∣3bc^(−) ∣=C_2 ^2 +2+3=6 ∣2bc∣=3,∣1bc∣=1 .Hence,in total we obtain ∣abc∣=∣9bc∣+∣8bc∣+∣7bc∣+6bc∣+∣5bc∣ +∣4bc∣+∣3bc∣+∣2bc∣+∣1bc∣= 45+36+28+21+15+10+6+4=165 numbers 3)The case abcd^(−) ∣abcd∣=∣9bcd∣+∣8bcd∣+...+∣3bcd∣+∣2bcd∣+∣1bcd∣ From above result we get: ∣9bcd∣=∣9cd∣+∣8cd∣...+∣1cd∣=45+36 28+21+15+10+6+4=165 ∣8bcd∣=∣8cd∣+...+∣1cd∣=165−45=120 ∣7bcd∣=∣8bcd∣−∣8cd∣=120−36=84 ∣6bcd∣=∣7bcd∣−∣7cd∣=84−28=56 ∣5bcd∣=∣6bcd∣−∣6cd∣=56−21=35 ∣4bcd∣=∣5bcd∣−∣5cd∣=35−15=20 ∣3bcd^(−) ∣= ∣4bcd∣−∣4cd∣=20−10=10 ∣2bcd∣=∣3bcd∣−∣3cd∣=10−6=4 ∣1bcd∣=∣2bcd∣−∣2cd∣=4−3=1 Hence,in total we obtain 165+120+84+56+35+20+10+5=495 4)The case abcde^(−) a)When 9 at first we have 9bcde^(−) From thepart 2)above we get ∣99cde^(−) ∣=∣9de∣+∣8de∣+∣7de∣+∣6de∣+∣5de∣+∣4de∣+∣3de∣ +∣5de∣+∣4de∣+∣3de∣+∣2de∣+∣1de∣ =45+36+28+21+15+10+6+4=165 ∣98cde∣=∣99cde∣−∣9de∣=165−45=120 ∣97cde∣=∣98cde∣−∣8de∣=120−36=84 ∣96cde∣=∣97cde∣−∣7de∣=84−28=56 ∣95cde∣=56−21=35,∣94cde∣=35−15=20 ∣93cde∣=10;∣92cde∣=4;∣91cde∣=1 .Hence,in the total we get 165+120+84+56+35+20+10+4+1 =495 numbers of forms 9bcde^(−) b)When 8 at the first place we have ∣8bcde^(−) ∣=∣88cde∣+∣87cde∣+...+∣81cde∣ =∣98cde∣+∣97cde∣+...+∣91cde∣ =∣9bcde∣−∣9cde∣=495−165=330 Brcause:See the formulas of part2) ∣88cde^(−) ∣=∣8de∣+∣7de∣+∣6de∣+∣5de∣ +∣4de∣+∣3de∣+∣2de∣+∣1de∣=165−45=120 ∣87cde∣=120−36=84 ∣86cde∣=84−28=56 ∣85cde∣=56−21=35 ∣84cde∣=35−15=20,∣83cde∣=10 ∣82cde∣=4,∣81cde∣=1,so in the total have 120+84+56+35+20+10+5=330 c)The case 7bcde^(−) we get (see the part3) ∣7bcde∣=∣8bcde∣−∣8cde∣ ∣=330−120=210 numbers d)The case 6bcde^(−) ;∣6bcde∣= ∣7bcde∣−∣7cde∣=210−84=126 e)The case5bcde^(−) ;∣ 5bcde^(−) ∣= ∣6bcde∣−∣6cde∣=126−56=70 f)The case 4bcde^(−) we get ∣4bcde∣=70−35=35 numbers g)The case 3bcde we get ∣3bcde∣=35−20=15 numbers ∣∣2bcde∣=15−10=5,∣1bcde∣=1 Finaly,in total we get 495+330+210+126+70+35+15+6= 1287 numbers of form abcde satisfy the condition a≥b≥c≥d≥e

For convenient we write \overset{―}{abcde} instead

of \overset{―}{x_{1} x_{2} x_{3} x_{4} x_{5}} and ∣ abcde ∣ - number of

numbers of form \overset{―}{abcde}

We solve the problem in turn for cases

1) How many are there the two - digit numbers

\overset{―}{ab} can be formed from the digits

1, . ., 9 such that a ⩾ b

This case, it is easy to see in the total

we can establish p = C_{9}^{2} + 9 = 45 ones

2) The case \overset{―}{abc} .

When 9 at first place we have

C_{8}^{2} + 8 + 9 = 45 numbers of form \overset{―}{9 bc}

Similarly, ∣ \overset{―}{8 bc} ∣= C_{7}^{2} + 7 + 8 = 36 ones

, \dots . ., ∣ \overset{―}{5 bc} ∣= C_{4}^{2} + 4 + 5 = 15 ones

∣ \overset{―}{4 bc} ∣= C_{3}^{2} + 3 + 4 = 10; ∣ \overset{―}{3 bc} ∣= C_{2}^{2} + 2 + 3 = 6

∣ 2 bc ∣= 3, ∣ 1 bc ∣= 1

. Hence, in total we obtain

∣ abc ∣=∣ 9 bc ∣ + ∣ 8 bc ∣ + ∣ 7 bc ∣ + 6 bc ∣ + ∣ 5 bc ∣

+ ∣ 4 bc ∣ + ∣ 3 bc ∣ + ∣ 2 bc ∣ + ∣ 1 bc ∣=

45 + 36 + 28 + 21 + 15 + 10 + 6 + 4 = 165 numbers

3) The case \overset{―}{abcd}

∣ abcd ∣=∣ 9 bcd ∣ + ∣ 8 bcd ∣ + \dots + ∣ 3 bcd ∣ + ∣ 2 bcd ∣ + ∣ 1 bcd ∣

From above result we get :

∣ 9 bcd ∣=∣ 9 cd ∣ + ∣ 8 cd ∣ \dots + ∣ 1 cd ∣= 45 + 36

28 + 21 + 15 + 10 + 6 + 4 = 165

∣ 8 bcd ∣=∣ 8 cd ∣ + \dots + ∣ 1 cd ∣= 165 - 45 = 120

∣ 7 bcd ∣=∣ 8 bcd ∣ - ∣ 8 cd ∣= 120 - 36 = 84

∣ 6 bcd ∣=∣ 7 bcd ∣ - ∣ 7 cd ∣= 84 - 28 = 56

∣ 5 bcd ∣=∣ 6 bcd ∣ - ∣ 6 cd ∣= 56 - 21 = 35

∣ 4 bcd ∣=∣ 5 bcd ∣ - ∣ 5 cd ∣= 35 - 15 = 20

∣ \overset{―}{3 bcd} ∣= ∣ 4 bcd ∣ - ∣ 4 cd ∣= 20 - 10 = 10

∣ 2 bcd ∣=∣ 3 bcd ∣ - ∣ 3 cd ∣= 10 - 6 = 4

∣ 1 bcd ∣=∣ 2 bcd ∣ - ∣ 2 cd ∣= 4 - 3 = 1

Hence, in total we obtain

165 + 120 + 84 + 56 + 35 + 20 + 10 + 5 = 495

4) The case \overset{―}{abcde}

a) When 9 at first we have \overset{―}{9 bcde}

From thepart 2) above we get

∣ \overset{―}{99 cde} ∣=∣ 9 de ∣ + ∣ 8 de ∣ + ∣ 7 de ∣ + ∣ 6 de ∣ + ∣ 5 de ∣ + ∣ 4 de ∣ + ∣ 3 de ∣

+ ∣ 5 de ∣ + ∣ 4 de ∣ + ∣ 3 de ∣ + ∣ 2 de ∣ + ∣ 1 de ∣

= 45 + 36 + 28 + 21 + 15 + 10 + 6 + 4 = 165

∣ 98 cde ∣=∣ 99 cde ∣ - ∣ 9 de ∣= 165 - 45 = 120

∣ 97 cde ∣=∣ 98 cde ∣ - ∣ 8 de ∣= 120 - 36 = 84

∣ 96 cde ∣=∣ 97 cde ∣ - ∣ 7 de ∣= 84 - 28 = 56

∣ 95 cde ∣= 56 - 21 = 35, ∣ 94 cde ∣= 35 - 15 = 20

∣ 93 cde ∣= 10; ∣ 92 cde ∣= 4; ∣ 91 cde ∣= 1

. Hence, in the total we get

165 + 120 + 84 + 56 + 35 + 20 + 10 + 4 + 1

= 495 numbers of forms \overset{―}{9 bcde}

b) When 8 at the first place we have

∣ \overset{―}{8 bcde} ∣=∣ 88 cde ∣ + ∣ 87 cde ∣ + \dots + ∣ 81 cde ∣

=∣ 98 cde ∣ + ∣ 97 cde ∣ + \dots + ∣ 91 cde ∣

=∣ 9 bcde ∣ - ∣ 9 cde ∣= 495 - 165 = 330

Brcause : See the formulas of part 2)

∣ \overset{―}{88 cde} ∣=∣ 8 de ∣ + ∣ 7 de ∣ + ∣ 6 de ∣ + ∣ 5 de ∣

+ ∣ 4 de ∣ + ∣ 3 de ∣ + ∣ 2 de ∣ + ∣ 1 de ∣= 165 - 45 = 120

∣ 87 cde ∣= 120 - 36 = 84

∣ 86 cde ∣= 84 - 28 = 56

∣ 85 cde ∣= 56 - 21 = 35

∣ 84 cde ∣= 35 - 15 = 20, ∣ 83 cde ∣= 10

∣ 82 cde ∣= 4, ∣ 81 cde ∣= 1, so in the total have

120 + 84 + 56 + 35 + 20 + 10 + 5 = 330

c) The case \overset{―}{7 bcde} we get (see the part 3)

∣ 7 bcde ∣=∣ 8 bcde ∣ - ∣ 8 cde ∣

∣= 330 - 120 = 210 numbers

d) The case \overset{―}{6 bcde}; ∣ 6 bcde ∣=

∣ 7 bcde ∣ - ∣ 7 cde ∣= 210 - 84 = 126

e) The case \overset{―}{5 bcde}; ∣ \overset{―}{5 bcde} ∣=

∣ 6 bcde ∣ - ∣ 6 cde ∣= 126 - 56 = 70

f) The case \overset{―}{4 bcde} we get

∣ 4 bcde ∣= 70 - 35 = 35 numbers

g) The case 3 bcde we get

∣ 3 bcde ∣= 35 - 20 = 15 numbers

∣∣ 2 bcde ∣= 15 - 10 = 5, ∣ 1 bcde ∣= 1

Finaly, in total we get

495 + 330 + 210 + 126 + 70 + 35 + 15 + 6 =

1287 numbers of form abcde satisfy

the condition a ⩾ b ⩾ c ⩾ d ⩾ e

Commented by prakash jain last updated on 13/Oct/20

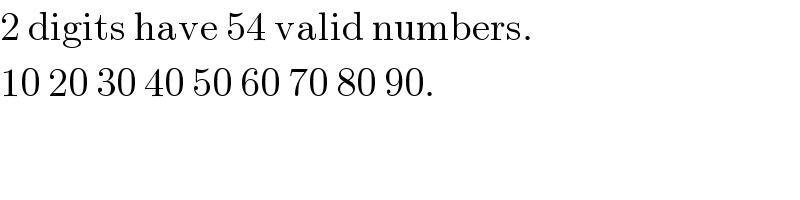
2 digits have 54 valid numbers. 10 20 30 40 50 60 70 80 90.

2 digits have 54 valid numbers .

10 20 30 40 50 60 70 80 90 .

Commented by 1549442205PVT last updated on 13/Oct/20

Here i just consider 9 digits 1,2...,9 case 10 digits is similar For 10 digits then ∣ab∣=C_(10) ^2 +10−1 since 00^(−) is rejected formula have given is always true

Here i just consider 9 digits 1, 2 \dots, 9

case 10 digits is similar

For 10 digits then

∣ ab ∣= C_{10}^{2} + 10 - 1 since \overset{―}{00} is rejected

formula have given is always true

Commented by prakash jain last updated on 13/Oct/20

determinant (((x_1 →),9,8,7,6,5,4,3,2,1),((1d),1,1,1,1,1,1,1,1,1),((2d),9,8,7,6,5,4,3,2,1),((3d),(45),(36),(28),(21),(15),(10),6,3,1),((4d),(165),(120),(84),(56),(35),(20),(10),4,1),((5d),(495),(330),(210),(126),(70),(35),(15),5,1),((6d),(1287),(792),(462),(252),(126),(56),(21),6,1)) The very first colums first digit for nd gives the same result as D(n−1) N(n,k)= n digits number with first digit as k N(n,k)=Σ_(j=0) ^k N(n−1,k)

| \begin{matrix} x_{1} \to & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1 \\ 1 d & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 2 d & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1 \\ 3 d & 45 & 36 & 28 & 21 & 15 & 10 & 6 & 3 & 1 \\ 4 d & 165 & 120 & 84 & 56 & 35 & 20 & 10 & 4 & 1 \\ 5 d & 495 & 330 & 210 & 126 & 70 & 35 & 15 & 5 & 1 \\ 6 d & 1287 & 792 & 462 & 252 & 126 & 56 & 21 & 6 & 1 \end{matrix} |

The very first colums first digit for n d gives

the same result as D (n - 1)

N (n, k) = n digits number with

first digit as k

N (n, k) = \underset{j = 0}{\sum^{k}} N (n - 1, k)

Commented by prakash jain last updated on 13/Oct/20

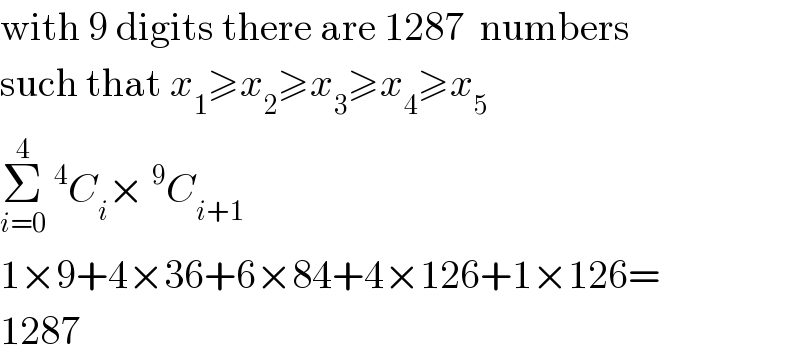
with 9 digits there are 1287 numbers such that x_1 ≥x_2 ≥x_3 ≥x_4 ≥x_5 Σ_(i=0) ^4 ^4 C_i ×^9 C_(i+1) 1×9+4×36+6×84+4×126+1×126= 1287

with 9 digits there are 1287 numbers

such that x_{1} ⩾ x_{2} ⩾ x_{3} ⩾ x_{4} ⩾ x_{5}

\underset{i = 0}{\sum^{4}}^{4} C_{i} \times^{9} C_{i + 1}

1 \times 9 + 4 \times 36 + 6 \times 84 + 4 \times 126 + 1 \times 126 =

1287

Commented by prakash jain last updated on 13/Oct/20

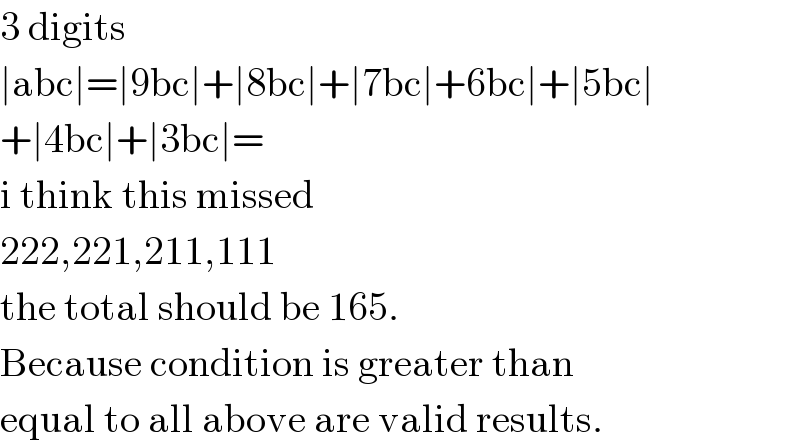
3 digits ∣abc∣=∣9bc∣+∣8bc∣+∣7bc∣+6bc∣+∣5bc∣ +∣4bc∣+∣3bc∣= i think this missed 222,221,211,111 the total should be 165. Because condition is greater than equal to all above are valid results.

3 digits

∣ abc ∣=∣ 9 bc ∣ + ∣ 8 bc ∣ + ∣ 7 bc ∣ + 6 bc ∣ + ∣ 5 bc ∣

+ ∣ 4 bc ∣ + ∣ 3 bc ∣=

i think this missed

222, 221, 211, 111

the total should be 165 .

Because condition is greater than

equal to all above are valid results .

Commented by prakash jain last updated on 13/Oct/20

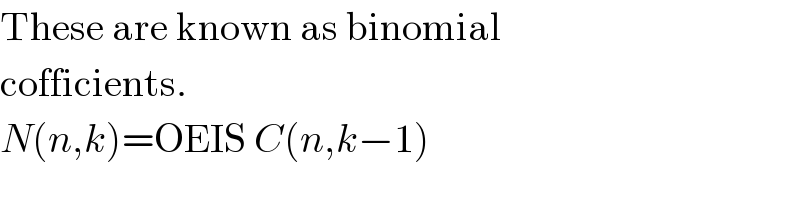
These are known as binomial cofficients. N(n,k)=OEIS C(n,k−1)

These are known as binomial

cofficients .

N (n, k) = OEIS C (n, k - 1)

Commented by prakash jain last updated on 13/Oct/20

http://oeis.org/A000581

Commented by mr W last updated on 13/Oct/20

t h a n k y o u a l l!

Commented by 1549442205PVT last updated on 14/Oct/20

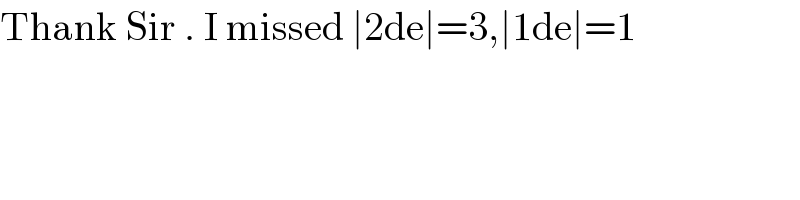
Thank Sir . I missed ∣ 2 de ∣= 3, ∣ 1 de ∣= 1

Answered by mr W last updated on 13/Oct/20

let′s see n digit numbers d_1 d_2 d_3 ...d_n with d_1 ≥d_2 ≥d_3 ≥...≥d_n . we select n_0 times 0, n_1 times 1, n_2 times 2, ..., n_9 times 9 to form such a number. n_0 +n_1 +n_2 +...+n_9 =n ...(i) with 0≤n_i for i=0,1,2,...,9. the number of valid n digit numbers is the number of integer solutions of (i). using generating function (1+x+x^2 +...)^(10) =(1/((1−x)^(10) ))=Σ_(k=0) ^∞ C_9 ^(k+9) x^k the coefficient of x^n term is the answer, which is C_9 ^(n+9) . since the number with n zeros is not valid, we get the final answer C_9 ^(n+9) −1. for 5 digit numbers the answer is C_9 ^(5+9) −1=2001.

{l e t}^{'} s s e e n d i g i t n u m b e r s d_{1} d_{2} d_{3} \dots d_{n}

w i t h d_{1} ⩾ d_{2} ⩾ d_{3} ⩾ \dots ⩾ d_{n} .

w e s e l e c t n_{0} t i m e s 0, n_{1} t i m e s 1,

n_{2} t i m e s 2, \dots, n_{9} t i m e s 9 t o f o r m s u c h

a n u m b e r .

n_{0} + n_{1} + n_{2} + \dots + n_{9} = n \dots (i)

w i t h 0 ⩽ n_{i} f o r i = 0, 1, 2, \dots, 9 .

t h e n u m b e r o f v a l i d n d i g i t n u m b e r s

i s t h e n u m b e r o f i n t e g e r s o l u t i o n s o f

(i) .

u s i n g g e n e r a t i n g f u n c t i o n

{(1 + x + x^{2} + \dots)}^{10} = \frac{1}{{(1 - x)}^{10}} = \underset{k = 0}{\sum^{\infty}} C_{9}^{k + 9} x^{k}

t h e c o e f f i c i e n t o f x^{n} t e r m i s t h e

a n s w e r, w h i c h i s C_{9}^{n + 9} . s i n c e t h e

n u m b e r w i t h n z e r o s i s n o t v a l i d,

w e g e t t h e f i n a l a n s w e r

C_{9}^{n + 9} - 1 .

f o r 5 d i g i t n u m b e r s t h e a n s w e r i s

C_{9}^{5 + 9} - 1 = 2001 .

Commented by mr W last updated on 13/Oct/20

e x a c t l y s i r!

Commented by mr W last updated on 13/Oct/20

Commented by prakash jain last updated on 13/Oct/20

After looking at your formula, i thought simplifying the result that i got Σ_(j=0) ^(n−1) ^(n−1) C_j ^(10) C_(j+1) =Σ_(j=0) ^(n−1) ^(n−1) C_j ^(10) C_(9−j) =A (1+x)^(9+n) =(1+x)^(n−1) (1+x)^(10) (1+x)^(9+n) =(^(n−1) C_0 +^(n−1) C_1 x+..+^(n−1) C_(n−1) x^(n−1) ) (^(10) C_0 +^(10) C_1 x+^(10) C_2 x^2 +..+^(10) C_(10) x^(10) ) A is same as coeffcient of x^9 in RHS from LHS coefficient of x^9 =^(9+n) C_9

After looking at your formula, i

thought simplifying the result that

i got

\underset{j = 0}{\sum^{n - 1}}^{n - 1} C_{j}^{10} C_{j + 1}

= \underset{j = 0}{\sum^{n - 1}}^{n - 1} C_{j}^{10} C_{9 - j} = A

{(1 + x)}^{9 + n} = {(1 + x)}^{n - 1} {(1 + x)}^{10}

{(1 + x)}^{9 + n} = (^{n - 1} C_{0} +^{n - 1} C_{1} x + . . +^{n - 1} C_{n - 1} x^{n - 1})

(^{10} C_{0} +^{10} C_{1} x +^{10} C_{2} x^{2} + . . +^{10} C_{10} x^{10})

A is same as coeffcient of x^{9} in RHS

from LHS coefficient of x^{9} =^{9 + n} C_{9}

Facebook Tweet Pin

Find-the-number-of-all-5-digit-numbers-x-1-x-2-x-3-x-4-x-5-with-x-1-x-2-x-3-x-4-x-5-

Leave a Reply Cancel reply