Find-the-number-of-solutions-for-positive-integers-x-y-z-satisfying-x-2y-3z-n-

Question Number 84182 by mr W last updated on 11/Mar/20

F i n d t h e n u m b e r o f s o l u t i o n s f o r

p o s i t i v e i n t e g e r s (x, y, z) s a t i s f y i n g

x + 2 y + 3 z = n .

Answered by mr W last updated on 10/Mar/20

M e t h o d 1

{l e t}^{'} s f i n d a t f i r s t t h e n u m b e r o f

s o l u t i o n s f o r x + 2 y = m w i t h m ⩾ 3 .

\Rightarrow 1 ⩽ y ⩽ ⌊ \frac{m - 1}{2} ⌋

i . e . t h e r e a r e ⌊ \frac{m - 1}{2} ⌋ s o l u t i o n s f o r

x + 2 y = m .

1 ⩽ z ⩽ ⌊ \frac{n - 3}{3} ⌋

m = n - 3 z

t o t a l n u m b e r o f s o l u t i o n s :

\Rightarrow N (n) = \underset{z = 1}{\sum^{⌊ \frac{n - 3}{3} ⌋}} ⌊ \frac{m - 1}{2} ⌋ = \underset{z = 1}{\sum^{⌊ \frac{n - 3}{3} ⌋}} ⌊ \frac{n - 3 z - 1}{2} ⌋

e x a m p l e s :

n = 6 : N = 1

n = 10 : N = 4

n = 55 : N = 225

n = 78 : N = 469

n = 1000 : N = 82834

Answered by mr W last updated on 10/Mar/20

M e t h o d 2

g e n e r a t i n g f u n c t i o n f o r x + 2 y + 3 z i s

\frac{x}{1 - x} \times \frac{x^{2}}{1 - x^{2}} \times \frac{x^{3}}{1 - x^{3}} = \frac{x^{6}}{(1 - x) (1 - x^{2}) (1 - x^{3})}

n u m b e r o f s o l u t i o n s o f x + 2 y + 3 z = n

i s t h e c o e f f i c i e n t o f x^{n} t e r m o f t h e

g e n e r a t i n g f u n c t i o n a b o v e .

t h e t a y l o r s e r i e s o f \frac{x^{6}}{(1 - x) (1 - x^{2}) (1 - x^{3})} :

Commented by mr W last updated on 10/Mar/20

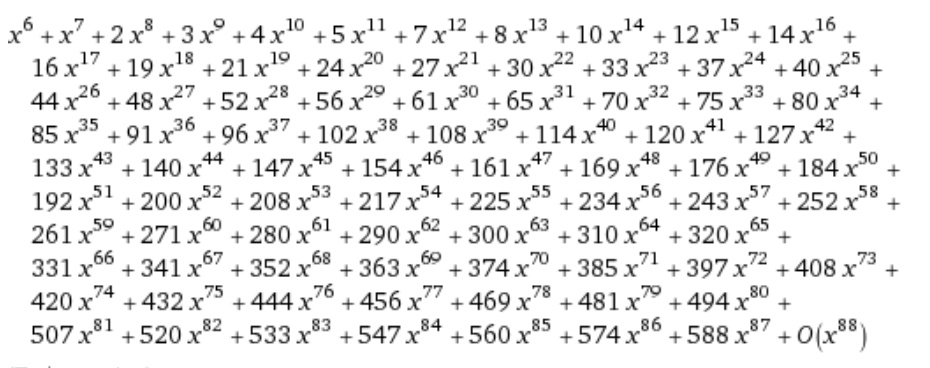
Commented by mr W last updated on 10/Mar/20

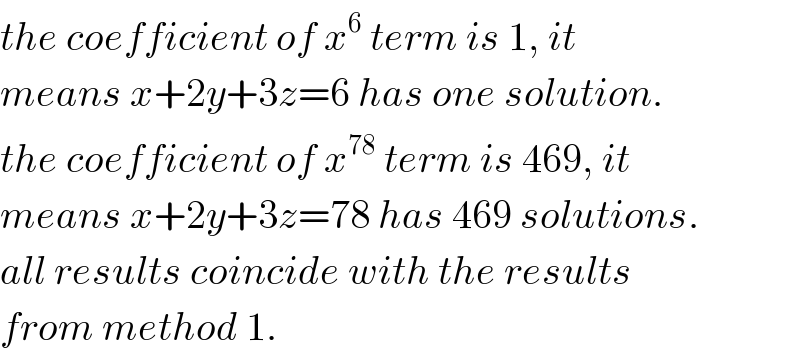
t h e c o e f f i c i e n t o f x^{6} t e r m i s 1, i t

m e a n s x + 2 y + 3 z = 6 h a s o n e s o l u t i o n .

t h e c o e f f i c i e n t o f x^{78} t e r m i s 469, i t

m e a n s x + 2 y + 3 z = 78 h a s 469 s o l u t i o n s .

a l l r e s u l t s c o i n c i d e w i t h t h e r e s u l t s

f r o m m e t h o d 1 .

Facebook Tweet Pin