Find-the-number-of-triangles-with-integer-side-lengths-and-perimeter-p-

Question Number 188301 by mr W last updated on 28/Feb/23

F i n d t h e n u m b e r o f t r i a n g l e s w i t h

i n t e g e r s i d e l e n g t h s a n d p e r i m e t e r p .

Commented by mr W last updated on 28/Feb/23

a s Q 188239, b u t i n g e n e r a l c a s e .

Commented by BaliramKumar last updated on 27/Feb/23

w h y

Commented by mr W last updated on 27/Feb/23

f o r m o r e s o l u t i o n s!

Commented by mr W last updated on 27/Feb/23

i f y o u h a v e a s o l u t i o n, p l e a s e s h a r e .

Answered by mr W last updated on 04/Mar/23

t h i s i s m y s o l u t i o n :

s a y t h e s i d e s o f t h e t r i a n g l e a r e a, b, c

w i t h a ⩽ b ⩽ c, t h e n t h e q u e s t i o n i s t o

f i n d t h e n u m b e r o f s o l u t i o n s o f

f o l l o w i n g e q u a t i o n

a + b + c = p \dots (i)

w i t h 1 ⩽ a ⩽ b ⩽ c a n d a + b > c .

s a y

a = 1 + u w i t h u ⩾ 0

b = a + v = 1 + u + v w i t h v ⩾ 0

c = b + w = 1 + u + v + w w i t h w ⩾ 0

a n d

(1 + u) + (1 + u + v) > (1 + u + v + w)

\Rightarrow u > w - 1 \Rightarrow u ⩾ w

s a y u = w + s w i t h s ⩾ 0

t h e n t h e e q u a t i o n (i) b e c o m e s t o

(1 + w + s) + (1 + w + s + v) + (1 + w + s + v + w) = p

\Rightarrow 3 + 4 w + 3 s + 2 v = p \dots (I)

w i t h w, s, v ⩾ 0

t h e n u m b e r o f s o l u t i o n s o f e q n . (I)

i s t h e c o e f f i c i e n t o f x^{p} t e r m i n

t h e e x p a n s i o n o f

x^{3} (1 + x^{4} + x^{8} + \dots) (1 + x^{3} + x^{6} + \dots) (1 + x^{2} + x^{4} + \dots)

i . e . \frac{x^{3}}{(1 - x^{4}) (1 - x^{3}) (1 - x^{2})} .

i t s e x p a n s i o n s e e b e l o w .

e x a m p l e s :

p = 16 : t h e c o e f . o f x^{16} i s 5 .

\Rightarrow 5 t r i a n g l e s h a v e p = 16 .

p = 50 : t h e c o e f . o f x^{50} i s 52 .

\Rightarrow 52 t r i a n g l e s h a v e p = 50 .

p = 75 : t h e c o e f . o f x^{75} i s 127 .

\Rightarrow 127 t r i a n g l e s h a v e p = 75 .

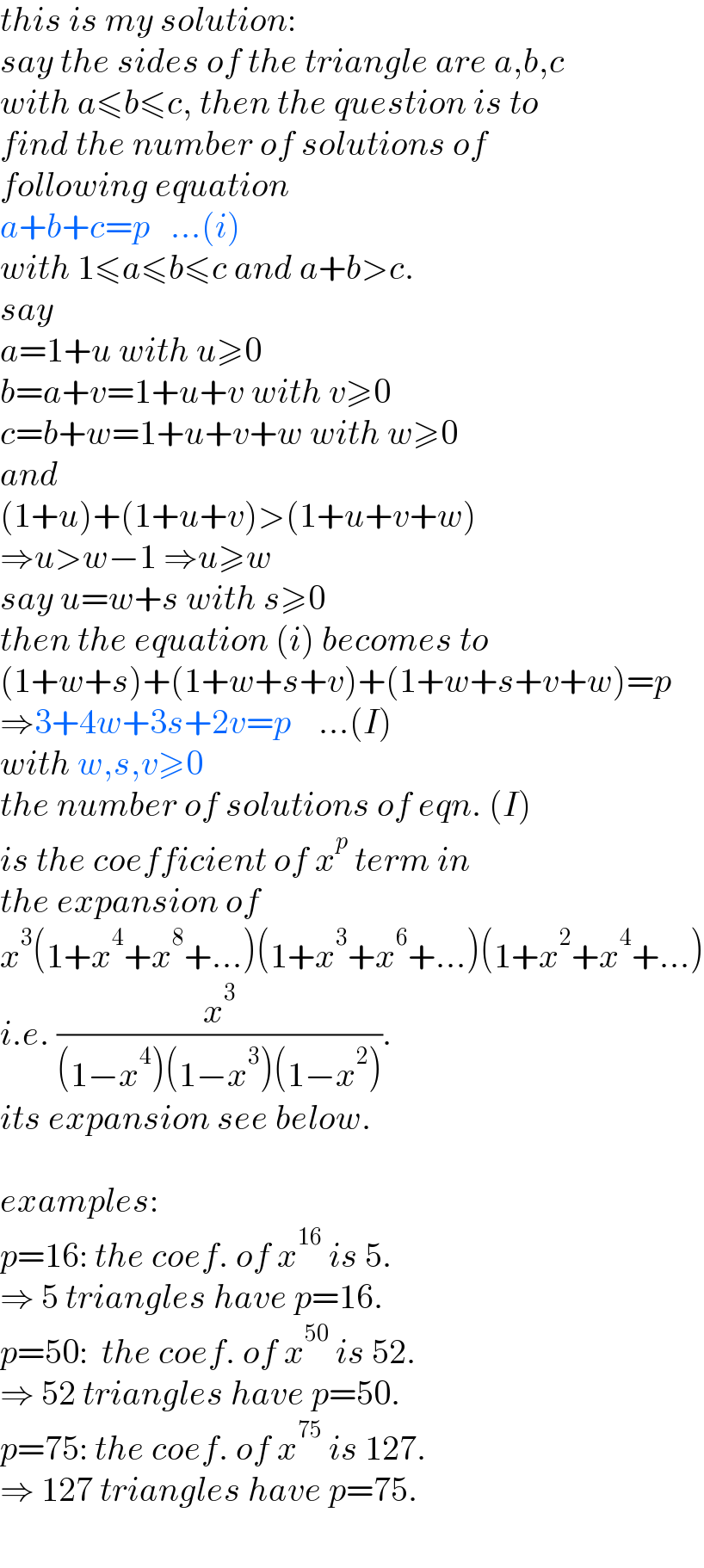
Commented by mr W last updated on 04/Mar/23

Commented by manxsol last updated on 27/Feb/23

B r a v o, S i r W . G r e a t w o r k .

t h a n k s f o r t h e e x p l a n a t i o n

Commented by mr W last updated on 28/Feb/23

t h i s i s a q u e s t i o n i n t h e n u m b e r

t h e o r y a b o u t t h e p a r t i t i o n o f a n

i n t e g e r .

Commented by mr W last updated on 28/Feb/23

Commented by BaliramKumar last updated on 28/Feb/23

G r e a t S i r