Question Number 101096 by student work last updated on 30/Jun/20
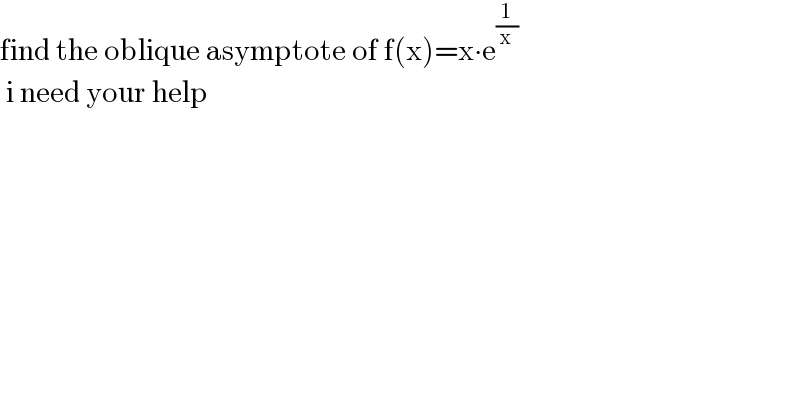
$$\mathrm{find}\:\mathrm{the}\:\mathrm{oblique}\:\mathrm{asymptote}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\centerdot\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:\:\:\:\: \\ $$$$\:\mathrm{i}\:\mathrm{need}\:\mathrm{your}\:\mathrm{help} \\ $$
Commented by student work last updated on 30/Jun/20

$$\mathrm{i}\:\mathrm{need}\:\mathrm{soon} \\ $$
Commented by student work last updated on 30/Jun/20

$$\mathrm{who}\:\mathrm{can}\:\mathrm{help}\:\mathrm{me}? \\ $$
Answered by mathmax by abdo last updated on 30/Jun/20
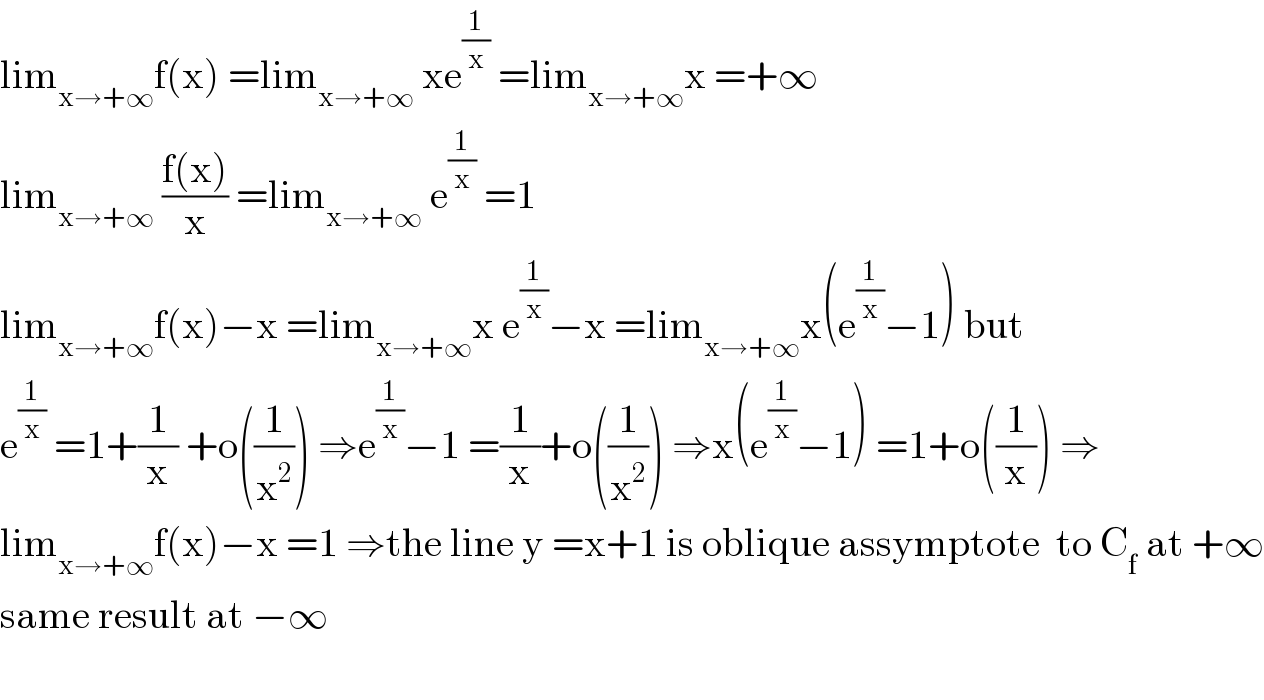
$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{xe}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\:=+\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{x}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\right)\:\mathrm{but} \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{x}\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\right)\:=\mathrm{1}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}\:=\mathrm{1}\:\Rightarrow\mathrm{the}\:\mathrm{line}\:\mathrm{y}\:=\mathrm{x}+\mathrm{1}\:\mathrm{is}\:\mathrm{oblique}\:\mathrm{assymptote}\:\:\mathrm{to}\:\mathrm{C}_{\mathrm{f}} \:\mathrm{at}\:+\infty \\ $$$$\mathrm{same}\:\mathrm{result}\:\mathrm{at}\:−\infty \\ $$$$ \\ $$
