Question Number 111209 by mathdave last updated on 02/Sep/20
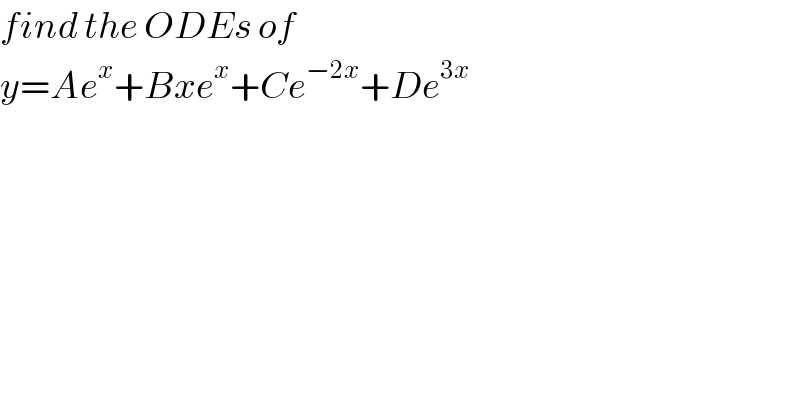
$${find}\:{the}\:{ODEs}\:{of}\: \\ $$$${y}={Ae}^{{x}} +{Bxe}^{{x}} +{Ce}^{−\mathrm{2}{x}} +{De}^{\mathrm{3}{x}} \\ $$
Commented by mohammad17 last updated on 02/Sep/20

$${can}\:{you}\:{solve} \\ $$
Commented by mohammad17 last updated on 02/Sep/20
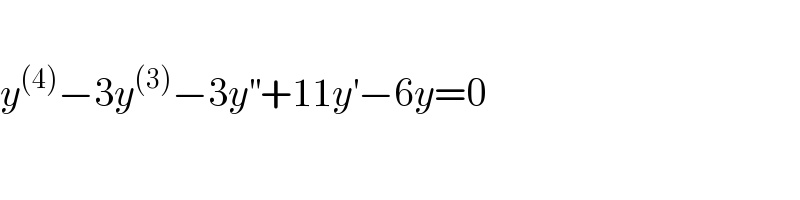
$$ \\ $$$${y}^{\left(\mathrm{4}\right)} −\mathrm{3}{y}^{\left(\mathrm{3}\right)} −\mathrm{3}{y}^{''} +\mathrm{11}{y}^{'} −\mathrm{6}{y}=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 02/Sep/20
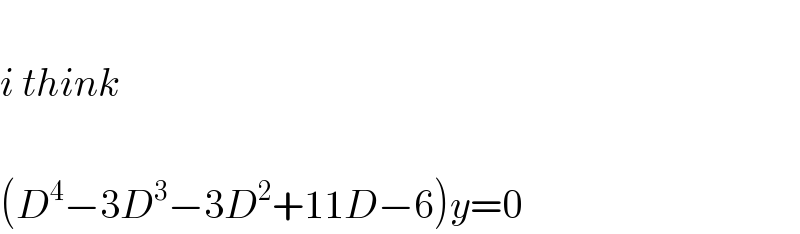
$$ \\ $$$${i}\:{think}\: \\ $$$$ \\ $$$$\left({D}^{\mathrm{4}} −\mathrm{3}{D}^{\mathrm{3}} −\mathrm{3}{D}^{\mathrm{2}} +\mathrm{11}{D}−\mathrm{6}\right){y}=\mathrm{0} \\ $$
Commented by mathdave last updated on 02/Sep/20

$${oh}\:{no}\: \\ $$
Commented by mathdave last updated on 02/Sep/20
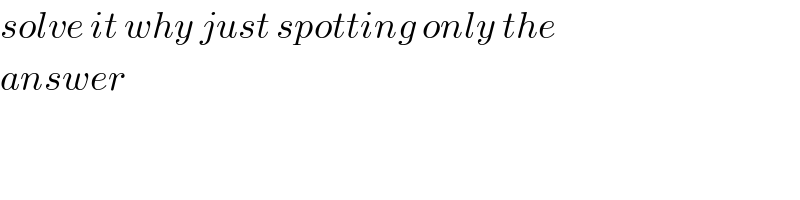
$${solve}\:{it}\:{why}\:{just}\:{spotting}\:{only}\:{the} \\ $$$${answer} \\ $$
Commented by mohammad17 last updated on 03/Sep/20
$${the}\:{solution}\:{is}\:{given}\:{by}\:{dirvaitive}\: \\ $$
