Question Number 32776 by NECx last updated on 02/Apr/18

$${Find}\:{the}\:{optimum}\:{points}\:{of} \\ $$$${the}\:{function}\:{y}={f}\left({x}\right) \\ $$$$\:\:{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{36}{x}+\mathrm{34} \\ $$
Answered by MJS last updated on 02/Apr/18
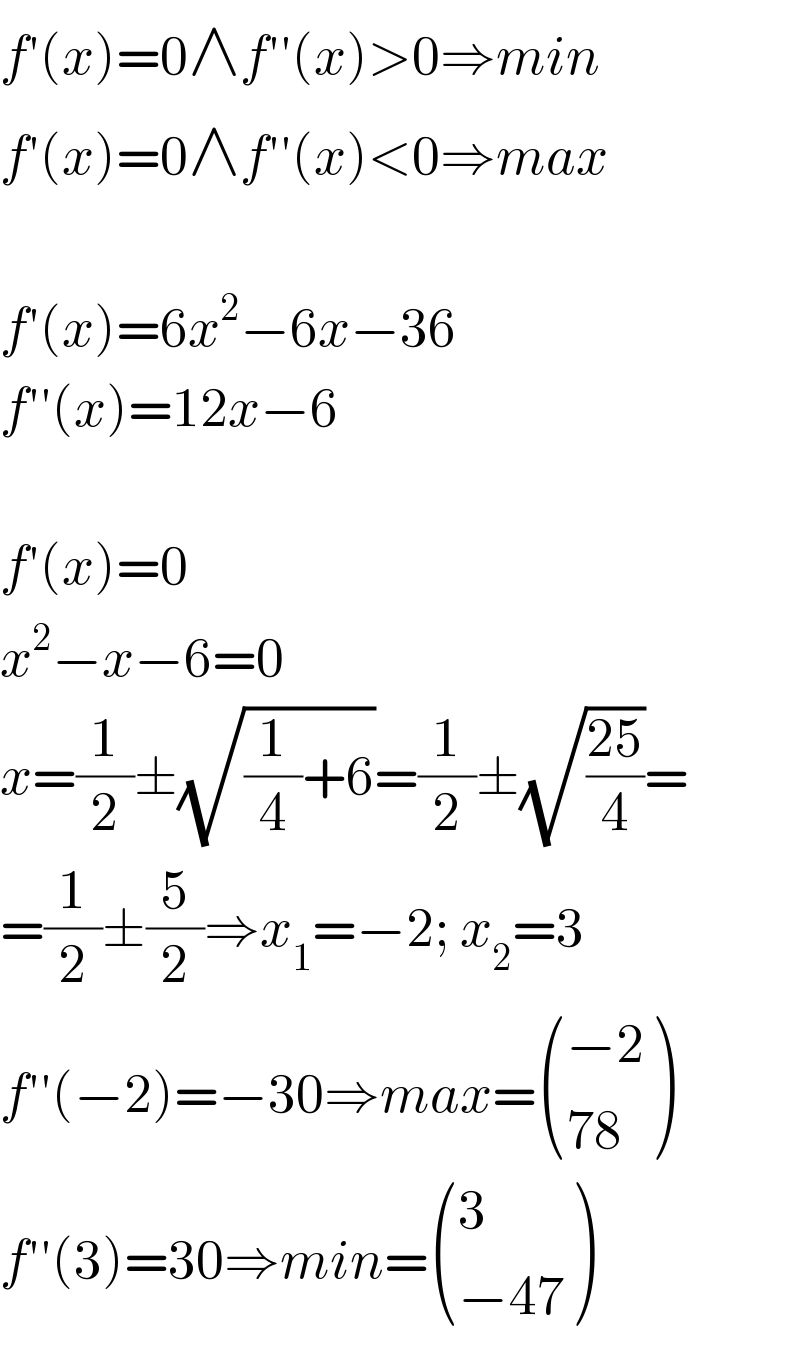
$${f}'\left({x}\right)=\mathrm{0}\wedge{f}''\left({x}\right)>\mathrm{0}\Rightarrow{min} \\ $$$${f}'\left({x}\right)=\mathrm{0}\wedge{f}''\left({x}\right)<\mathrm{0}\Rightarrow{max} \\ $$$$ \\ $$$${f}'\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{36} \\ $$$${f}''\left({x}\right)=\mathrm{12}{x}−\mathrm{6} \\ $$$$ \\ $$$${f}'\left({x}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{6}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{25}}{\mathrm{4}}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{5}}{\mathrm{2}}\Rightarrow{x}_{\mathrm{1}} =−\mathrm{2};\:{x}_{\mathrm{2}} =\mathrm{3} \\ $$$${f}''\left(−\mathrm{2}\right)=−\mathrm{30}\Rightarrow{max}=\begin{pmatrix}{−\mathrm{2}}\\{\mathrm{78}}\end{pmatrix} \\ $$$${f}''\left(\mathrm{3}\right)=\mathrm{30}\Rightarrow{min}=\begin{pmatrix}{\mathrm{3}}\\{−\mathrm{47}}\end{pmatrix} \\ $$
Commented by NECx last updated on 02/Apr/18
$${thank}\:{you}\:{so}\:{much} \\ $$
