Question Number 18470 by tawa tawa last updated on 22/Jul/17
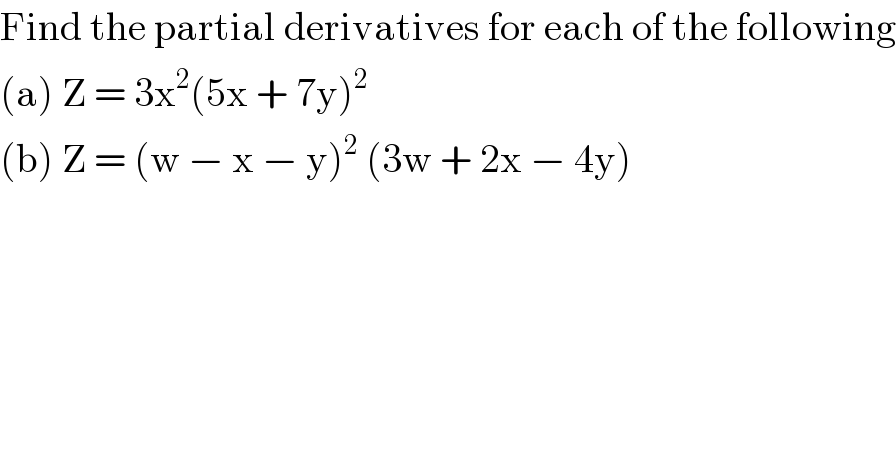
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{partial}\:\mathrm{derivatives}\:\mathrm{for}\:\mathrm{each}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Z}\:=\:\mathrm{3x}^{\mathrm{2}} \left(\mathrm{5x}\:+\:\mathrm{7y}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Z}\:=\:\left(\mathrm{w}\:−\:\mathrm{x}\:−\:\mathrm{y}\right)^{\mathrm{2}} \:\left(\mathrm{3w}\:+\:\mathrm{2x}\:−\:\mathrm{4y}\right) \\ $$
Answered by ajfour last updated on 22/Jul/17
![(a) (∂z/∂x)=6x(5x+7y)^2 +3x^2 [2(5x+7y)(5)] =6x(5x+7y)(10x+7y) (∂z/∂y)=3x^2 (2)(5x+7y)(7) =42x^2 (5x+7y) (b) (∂z/∂x)=−2(w−x−y)(3w+2x−4y) +2(w−x−y)^2 =−2(w−x−y)(2w+3x−3y) (∂z/∂y)=−2(w−x−y)(3w+2x−4y) −4(w−x−y)^2 =−2(w−x−y)(5w−6y) (∂z/∂w)=2(w−x−y)(3w+2x−4y) +3(w−x−y)^2 =(w−x−y)(9w+x−11y) .](https://www.tinkutara.com/question/Q18485.png)
$$\:\left(\mathrm{a}\right) \\ $$$$\:\frac{\partial\mathrm{z}}{\partial\mathrm{x}}=\mathrm{6x}\left(\mathrm{5x}+\mathrm{7y}\right)^{\mathrm{2}} +\mathrm{3x}^{\mathrm{2}} \left[\mathrm{2}\left(\mathrm{5x}+\mathrm{7y}\right)\left(\mathrm{5}\right)\right] \\ $$$$\:\:\:\:\:\:\:=\mathrm{6x}\left(\mathrm{5x}+\mathrm{7y}\right)\left(\mathrm{10x}+\mathrm{7y}\right) \\ $$$$\frac{\partial\mathrm{z}}{\partial\mathrm{y}}=\mathrm{3x}^{\mathrm{2}} \left(\mathrm{2}\right)\left(\mathrm{5x}+\mathrm{7y}\right)\left(\mathrm{7}\right) \\ $$$$\:\:\:\:\:=\mathrm{42x}^{\mathrm{2}} \left(\mathrm{5x}+\mathrm{7y}\right) \\ $$$$ \\ $$$$\left(\mathrm{b}\right)\:\:\frac{\partial\mathrm{z}}{\partial\mathrm{x}}=−\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{3w}+\mathrm{2x}−\mathrm{4y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{2w}+\mathrm{3x}−\mathrm{3y}\right) \\ $$$$\:\frac{\partial\mathrm{z}}{\partial\mathrm{y}}=−\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{3w}+\mathrm{2x}−\mathrm{4y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{5w}−\mathrm{6y}\right) \\ $$$$\frac{\partial\mathrm{z}}{\partial\mathrm{w}}=\mathrm{2}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{3w}+\mathrm{2x}−\mathrm{4y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{3}\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{w}−\mathrm{x}−\mathrm{y}\right)\left(\mathrm{9w}+\mathrm{x}−\mathrm{11y}\right)\:. \\ $$
Commented by tawa tawa last updated on 22/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
