Question Number 97115 by bobhans last updated on 06/Jun/20

$$\mathrm{find}\:\mathrm{the}\:\mathrm{points}\:\mathrm{on}\:\mathrm{hyperbola}\:\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{closest}\:\mathrm{to}\:\mathrm{point}\:\left(\mathrm{0},\mathrm{1}\right)\: \\ $$
Answered by mr W last updated on 06/Jun/20
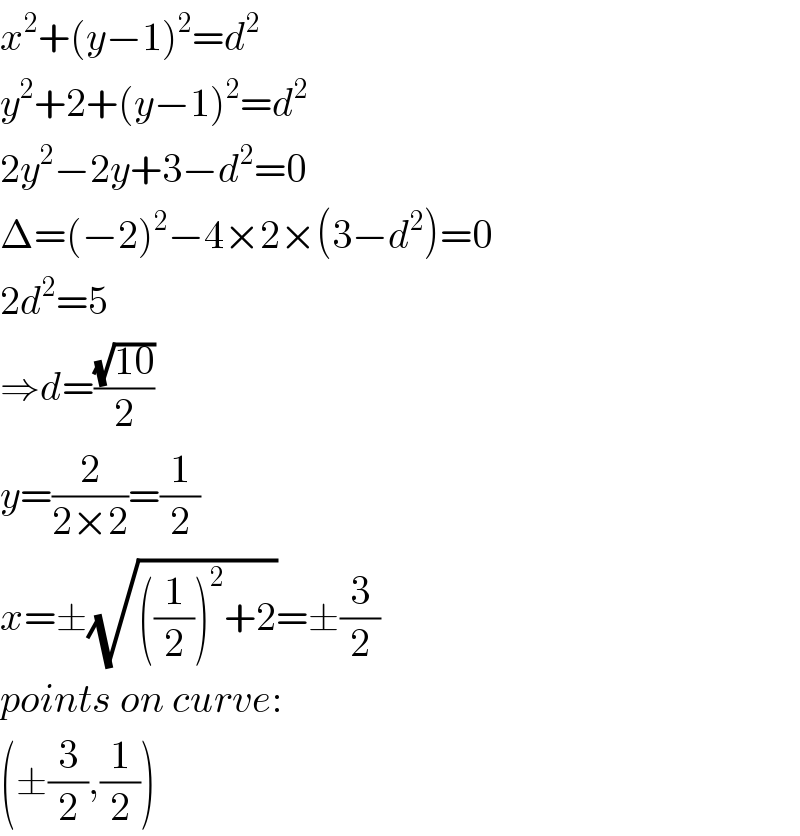
$${x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} +\mathrm{2}+\left({y}−\mathrm{1}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{3}−{d}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{2}×\left(\mathrm{3}−{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{2}{d}^{\mathrm{2}} =\mathrm{5} \\ $$$$\Rightarrow{d}=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{2}}{\mathrm{2}×\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}=\pm\sqrt{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}}=\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${points}\:{on}\:{curve}: \\ $$$$\left(\pm\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by bobhans last updated on 06/Jun/20
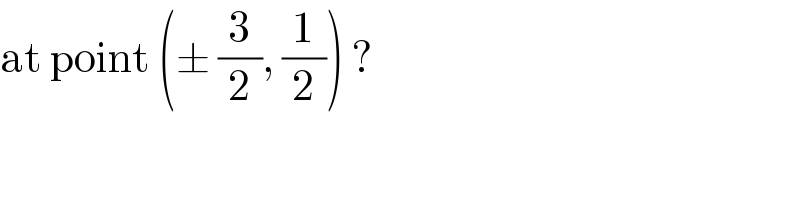
$$\mathrm{at}\:\mathrm{point}\:\left(\pm\:\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{2}}\right)\:? \\ $$
Commented by bobhans last updated on 06/Jun/20

$$\mathrm{oo}\:\mathrm{yes}.\: \\ $$
